Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
PT hoành đồ giao điểm của (C) và trục hoành:
x3 + 3x2 + mx + m - 2 = 0 (1)
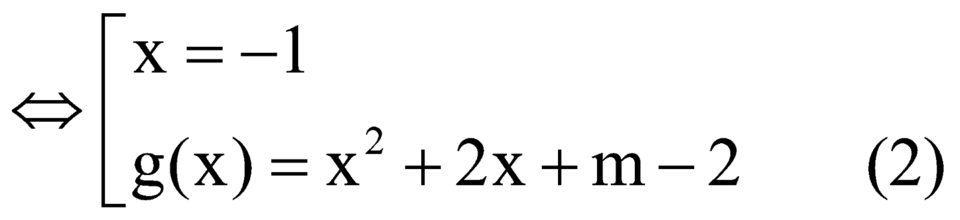
(Cm) có 2 điểm cực trị nằm về hai phía đối với trục Ox
PT (1) có 3 nghiệm phân biệt
(2) có 2 nghiêm phân biệt khác -1
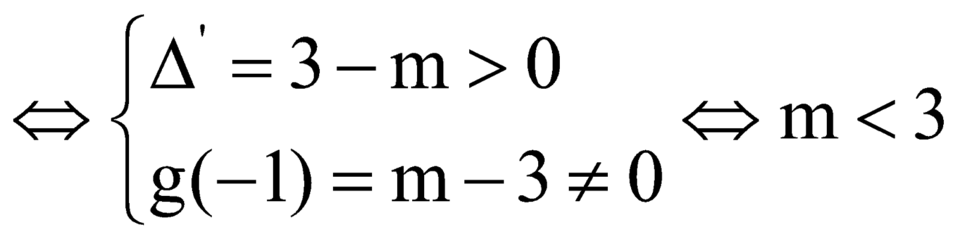
Đáp án C
y ' = x 2 − 6 m x ; y ' = 0 ⇔ x 1 = 0 x 2 = 6 m .
Đồ thị hàm số có điểm cực đại, cực trị ⇔ y ' = 0 có hai nghiệm phân biệt ⇔ m ≠ 0 .
Các điểm cực trị nằm về hai phía của trục hoành ⇔ y 1 y 2 < 0
⇔ m − 36 m 3 + m < 0 ⇔ m 2 − 36 m 2 + 1 < 0 ⇔ m > 1 6 .
Chọn đáp án B
Hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành là nghiệm của phương trình :
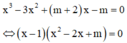
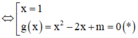
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục hoành
Phương trình (*) có hai nghiệm phân biệt khác 1
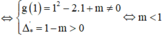
Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
Hai điểm cực trị có hoành độ dương
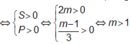
Vậy các giá trị cần tìm của m là m >1
1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)
Đáp án A.
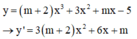
Hàm số đã cho có điểm cực đại và điểm cực tiểu đều có hoành độ dương
· Đường tròn
C m : x 2 + y 2 - 2 m x - 4 m y + 5 m 2 - 1 = 0
có tâm I ( m;2m ), bán kính R = 1.Ta có:
I B = 5 m 2 + 4 m + 8 = 5 m + 2 5 2 + 36 5 ≥ 6 5 > 1 = R
điểm B nằm ở phía ngoài đường tròn C m . Do đó điểm A nằm ở phía trong đường tròn C m , tức là:
L A < 1 = R ⇔ 5 m 2 - 8 m + 4 < 1 ⇔ 5 m 2 - 8 m + 3 < 0 ⇔ 3 5 < m < 1
Đáp án C
Đạo hàm y’ = 3x2+6x+m. Ta có ∆ ' y ' = 9 - 3 m
Hàm số có cực đại và cực tiểu khi ∆ ' y ' = 9 - 3 m > 0 ⇔ m < 3
Ta có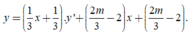
Gọi x1; x2 là hoành độ của hai điểm cực trị khi đó
Theo định lí Viet, ta có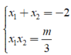
Hai điểm cực trị nằm về hai phía trục hoành khi y1.y2<0
Chọn C.