cho (O) đường kính AB ,C di động trên nửa đường tròn đó.vẽ (I) tiếp xúc với (O) tại C và tiep xúc vs đường kính AB tại D.dduwong tron này cắt AC,BC lan luot tai M,N....cmr: a) M,I,N thẳng hàng b) ID vuong goc voi MN. c) CD đi qua 1 đ' co dinh.Từ đó suy ra cách dựng đg tròn (I)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 12 2015
vẽ nữa (O) kia. vẽ đường kính COK.gọi giao điểm của EM vs CK là F. ta có: tam giác CEK nội tiếp (O), có CK là đường kính => tam giác CEK vuông tại E, có đường cao EF => = CF.CK(1)
ta có: tam giác CMF Đồng dạng với tam giác COH(g.g)
=> \(\frac{CM}{OC}=\frac{CF}{CH}\Rightarrow\frac{CH}{CK}=\frac{CF}{CH}\Rightarrow CH^2=CK.CF\left(2\right)\)
=> từ (1);(2)=> CE=CH. mà ta dễ dàng c/m được CE=CD. vậy CH = CD, nên H thuộc (O;CD). mà CH vuông góc với AB. => dpcm
21 tháng 1 2016
b, Cm : MN // AB
(I) tiếp xúc AB tại d => ID vuông góc AB
=> ID vuông góc với MN
c, thì chưa nghĩ ra
21 tháng 1 2016
tam giác ICN cân
tam giác COB cân
=> cặp góc đồng vị bằng nhau
=> IN // AB => MN // AB
CM
7 tháng 8 2018
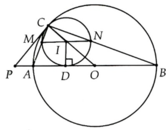
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm
7 tháng 12 2021
Vì góc ACB là có nội tiếp chắn nửa đường tròn của (O)
=> góc ACB= 90 độ
Xét (I) có góc MCN là góc nội tiếp chắn cung MN
mà góc MCN= 90 độ
=> MN là đường kính của (I)
=> 3 điểm M,I,N thẳng hàng
b) vì Δ CIN cân tại I( IC=IN=R)
=> góc ICN= góc INC
lại có Δ COB cân tại O(OC=OB=R)
=> góc OCB= góc OBC
=> góc INC= góc OBC ( cùng = góc OCB)
mà 2 góc này ở vị trí đồng vị của 2 đường thẳng MN và AB
=> MN // AB
lại có ID vuông góc với AB
=> ID vuông góc với MN( đpcm)
Trong câu hỏi tương tự ko có mà Nguyễn Văn Tuấn