Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b, Cm : MN // AB
(I) tiếp xúc AB tại d => ID vuông góc AB
=> ID vuông góc với MN
c, thì chưa nghĩ ra
tam giác ICN cân
tam giác COB cân
=> cặp góc đồng vị bằng nhau
=> IN // AB => MN // AB

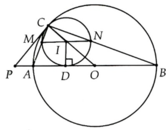
a, Vẽ tiếp tuyến tại C cắt đường AB ở P. Phân giác C P B ^ cắt OC ở I. Vẽ đường tròn tâm I bán kính IC, đó là đường tròn cần tìm
b, Do A C B ^ = 90 0 nên M C N ^ = 90 0
=> MN là đường kính của (I) => ĐPCM
c, Chứng minh được MN//AB nên ID ^ MN => M D ⏜ = N D ⏜ hay CD là tia phân giác A C B ^ => Đpcm

Vì góc ACB là có nội tiếp chắn nửa đường tròn của (O)
=> góc ACB= 90 độ
Xét (I) có góc MCN là góc nội tiếp chắn cung MN
mà góc MCN= 90 độ
=> MN là đường kính của (I)
=> 3 điểm M,I,N thẳng hàng
b) vì Δ CIN cân tại I( IC=IN=R)
=> góc ICN= góc INC
lại có Δ COB cân tại O(OC=OB=R)
=> góc OCB= góc OBC
=> góc INC= góc OBC ( cùng = góc OCB)
mà 2 góc này ở vị trí đồng vị của 2 đường thẳng MN và AB
=> MN // AB
lại có ID vuông góc với AB
=> ID vuông góc với MN( đpcm)
vẽ nữa (O) kia. vẽ đường kính COK.gọi giao điểm của EM vs CK là F. ta có: tam giác CEK nội tiếp (O), có CK là đường kính => tam giác CEK vuông tại E, có đường cao EF => = CF.CK(1)
ta có: tam giác CMF Đồng dạng với tam giác COH(g.g)
=> \(\frac{CM}{OC}=\frac{CF}{CH}\Rightarrow\frac{CH}{CK}=\frac{CF}{CH}\Rightarrow CH^2=CK.CF\left(2\right)\)
=> từ (1);(2)=> CE=CH. mà ta dễ dàng c/m được CE=CD. vậy CH = CD, nên H thuộc (O;CD). mà CH vuông góc với AB. => dpcm