Cho phương trình m 2 - 3 m 2 x m 2 4 m 5 = 0 . Tìm tất cả các giá trị thực của tham số m để phương trì...

PT

Pham Trong Bach

12 tháng 9 2017

Cho phương trình m 2 - 3 m + 2 x + m 2 + 4 m + 5 = 0 . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm đúng với mọi x thuộc R. A. m = −2. B. m = −5. C. m = 1. D. Không tồn...

Đọc tiếp

#Toán lớp 10

1

CM

Cao Minh Tâm

12 tháng 9 2017

Phương trình đã cho nghiệm đúng với hay phương trình có vô số nghiệm khi

m 2 − 3 m + 2 = 0 − ( m 2 + 4 m + 5 ) = 0 ⇔ m = 1 m = 2 m ∈ ∅ ⇔ m ∈ ∅

Đáp án cần chọn là: D

Đúng(0)

K

Kuramajiva

14 tháng 12 2020

Câu 1: Tìm tất cả các giá trị cuả tham số m để phương trình \(4\sqrt{x^2-4x+5} =x^2-4x+2m-1\) có 4 nghiệm phân biệt Câu 2: Tìm các giá trị của tham số m sao cho tổng các bình phương hai nghiệm của phương trình \((m-3)x^2+2x-4=0\) bằng 4 Câu 3: Cho tam giác ABC có \(BC=a, AC=b, AB=c\) và I là tâm đường tròn nội tiếp tam giác. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\) Câu 4: Cho tam...

Đọc tiếp

#Toán lớp 10

4

NV

Nguyễn Việt Lâm

Giáo viên

14 tháng 12 2020

1.

Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)

Pt trở thành:

\(4t=t^2-5+2m-1\)

\(\Leftrightarrow t^2-4t+2m-6=0\) (1)

Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

14 tháng 12 2020

2.

Để pt đã cho có 2 nghiệm:

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)

Khi đó:

\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)

\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)

\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)

Đúng(0)

HB

hạ băng

17 tháng 8 2021

1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm...

Đọc tiếp

#Toán lớp 11

0

ND

Nguyễn Đình Hữu

24 tháng 11 2021

tìm tất cả các giá trị thực của tham số m để phương trình x-4√(x+3 ) + m = 0 có 2 nghiệm phân biệt

#Toán lớp 10

1

MY

missing you =

24 tháng 11 2021

\(x-4\sqrt{x+3}+m=0\)

\(\Leftrightarrow x+3-4\sqrt{x+3}-3+m=0\left(1\right)\)

\(đăt:\sqrt{x+3}=t\left(t\ge0\right)\)

\(\left(1\right)\Leftrightarrow t^2-4t-3+m=0\Leftrightarrow f\left(t\right)=t^2-4t-3=-m\left(2\right)\)

\(\left(1\right)-có-2ngo-phân-biệt\Leftrightarrow\left(2\right)có-2ngo-phân-biệt-thỏa:t\ge0\)

\(\Rightarrow f\left(0\right)=-3\)

\(\Rightarrow f\left(t\right)min=\dfrac{-\Delta}{4a}=-7\Leftrightarrow t=2\)

\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)

Đúng(2)

MY

missing you =

15 tháng 12 2021

\(t^2-4t-3+m=0\Leftrightarrow t^2-4t-3=-m\)

\(có-2nghiệm-pb-trên[0;\text{+∞})\)

\(xét-bảng-biến-thiên-củaf\left(t\right)=t^2-4t-3,trên[0;\text{+∞})\)

dựa vào bảng biến thiên ta thấy số nghiệm của phương trình f(t)

là số giao điểm của đường thẳng y=-m

\(\Rightarrow-7< -m\le-3\Leftrightarrow3\le m< 7\)

Đúng(1)

DT

Di Thiên

8 tháng 2 2021

Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm : a) x^2 - 8√x^2+1 +5-m=0 b) x^2 + 2x - 8√x^2+2x+5 +3-m =0

#Toán lớp 10

0

HH

Hug Hug - 3 cục bánh bao của Hội Bạ...

7 tháng 4 2022

tìm tất cả các giá trị thực của tham số m để phương trình \(^{x^2-2x+\sqrt{-x^2+2x}-3+m=0}\) có nghiệm

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

8 tháng 4 2022

Đặt \(-x^2+2x=t\Rightarrow0\le t\le1\)

\(\Rightarrow-t^2+t-3+m=0\)

\(\Leftrightarrow t^2-t+3=m\)

Xét hàm \(f\left(t\right)=t^2-t+3\) trên \(\left[0;1\right]\)

\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)

\(f\left(0\right)=3\) ; \(f\left(1\right)=3\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{11}{4}\)

\(\Rightarrow\dfrac{11}{4}\le f\left(t\right)\le3\)

\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(\dfrac{11}{4}\le m\le3\)

Đúng(0)

PT

Pham Trong Bach

30 tháng 10 2017

Cho phương trình m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 < x1 < 1 < x2 A. 2 ; + ∞ B. - 1 ; 2 C. - ∞ ; - 1 D. - ∞ ; ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

30 tháng 10 2017

Đáp án B.

Đặt t = log₂ x,

khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0

⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).

Để phương trình (*) có hai nghiệm phân biệt

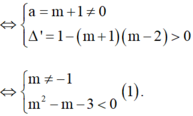
Khi đó gọi x₁, x₂ lần lượt hai nghiệm của phương trình (*).

Vì 0 < x₁ < 1 < x₂ suy ra

Đúng(0)

NH

Nguyễn Hoàng Khang

24 tháng 12 2021

Câu 1. Tìm tất cả các giá trị thực của tham sốmđể phương trình 2m x m    4 3 6vô nghiệm.A.m 1.B.m  2.C.m  2.D.m  2.Câu 2. Tìm tất cả các giá trị thực của tham sốmđể phương trìnhmx m  0vô nghiệm.A.m.B.m  0 . C.m . D.m .Câu 3. Tìm giá trị thực của tham sốmđể phương trình 2 2m m x m m     5 6 2vô nghiệm.A.m 1.B.m  2.C.m  3.D.m  6.Câu 4. Cho phương...

Đọc tiếp

Câu 1. Tìm tất cả các giá trị thực của tham số
m
để phương trình
 
2
m x m    4 3 6

vô nghiệm.

A.
m 1.

B.
m  2.

C.
m  2.

D.
m  2.

Câu 2. Tìm tất cả các giá trị thực của tham số
m
để phương trình

mx m  0

vô nghiệm.

A.
m.
B.
m  0 . 

C.
m .
 

D.
m .

Câu 3. Tìm giá trị thực của tham số
m
để phương trình

 
2 2
m m x m m     5 6 2

vô nghiệm.

A.
m 1.

B.
m  2.

C.
m  3.

D.
m  6.

Câu 4. Cho phương trình

   
2
m x m x m      1 1 7 5

. Tìm tất cả các giá trị thực của tham số
m
để phương trình đã cho vô

nghiệm.
A.
m 1.

B.
m m   2; 3.
C.
m  2.

D.
m  3.

Câu 6. Tìm tất cả các giá trị thực của tham số
m
để phương trình

2 4 2 m x m    

có nghiệm duy nhất.

A.
m  1.
B.
m  2.

C.
m  1.

D.
m  2.

Trang 24
Câu 11. Tìm tất cả các giá trị thực của tham số để phương trình có nghiệm đúng với mọi thuộc
A. B. C. D.

Vấn đề 2. SỐ NGHIỆM CỦA PHƯƠNG TRÌNH BẬC HAI

Câu 16. Phương trình
2
ax bx c    0

có nghiệm duy nhất khi và chỉ khi:

A.
a  0.

B.
0
0
a 

 
hoặc
0
.
0
a
b
 

 

C.
abc    0.

D.
0
.
0
a 

 

Câu 17. Số 1

là nghiệm của phương trình nào trong các phương trình sau?

A.
2
x x    4 2 0.

B.
2
2 5 7 0. x x   

C.
2
    3 5 2 0. x x

D.
3
x  1 0.

Câu 20. Phương trình vô nghiệm khi:
A. B. C. D.
Câu 22. Phương trình có nghiệm kép khi:
A. B. C. D.
m

2 m x m 1 1 x .

m 1. m 1. m 1. m 0. 2 m x mx m 1 2 2 0 m 2. m 2. m 2. m 2. 2 m x x – 2 2 –1 0 m m 1; 2. m 1. m 2. m 1.

Trang 25
Câu 23. Phương trình có nghiệm duy nhất khi:
A. B. C. D.
Câu 24. Phương trình có nghiệm duy nhất khi:
A. B. C. D.
Câu 25. Phương trình có nghiệm kép khi:
A. B. C. D.

Vấn đề 3. DẤU CỦA NGHIỆM PHƯƠNG TRÌNH BẬC HAI

Câu 41. Phương trình

 

2
ax bx c a     0 0

có hai nghiệm phân biệt cùng dấu khi và chỉ khi:

A.
0
.
P 0
  
 

B.
0
.
P 0
  
 

C.
0
.
S 0
  
 

D.
0
.
S 0
  
 

Câu 42. Phương trình

 

2
ax bx c a     0 0

có hai nghiệm âm phân biệt khi và chỉ khi:

A.
0
.
P 0
  
 

B.
0
0.
0
P
S
  
 

 

C.
0
0.
0
P
S
  
 

 

D.
0
.
S 0
  
 
2 mx x m 6 4 3 m . m 0. m . m 0. 2 mx m x m – 2 1 1 0 m 0. m 1. m m 0; 1. m 1. 2 m x m x m 1 – 6 1 2 3 0 m 1. 6

1;
7
m m

6
.
7
m

Trang 26
Câu 43. Phương trình

 

2
ax bx c a     0 0

có hai nghiệm dương phân biệt khi và chỉ khi:

A.
0
.
P 0
  
 

B.
0
0.
0
P
S
  
 

 

C.
0
0.
0
P
S
  
 

 

D.
0
.
S 0
  
 

Câu 44. Phương trình

 

2
ax bx c a     0 0

có hai nghiệm trái dấu khi và chỉ khi:

A.
0
.
S 0
  
 

B.
0
.
S 0
  
 

C.
P  0.

D.
P  0.

Câu 45. Phương trình
2
x mx   1 0

có hai nghiệm âm phân biệt khi:

A.
m  2.
B.
m  2.

C.
m  2.

D.
m  0.

#Toán lớp 10

0

TP

(:!Tổng Phước Yaru!:)

21 tháng 3 2022

Tìm tất cả các giá trị thực của tham số m để phương trình ( m² - 4 ) x⁴+ ( m - 2 ) x ²+ 1 = 0. Có đúng hai nghiệm phân biệt.!!

#Toán lớp 10

2

TP

(:!Tổng Phước Yaru!:)

21 tháng 3 2022

cíu!!!

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

21 tháng 3 2022

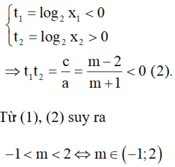
Trường hợp 1: \(m\ne\pm2\)

Để phương trình có đúng hai nghiệm phân biệt thì phương trình này sẽ có hai nghiệm trái dấu

=>\(m^2-4< 0\)

hay -2<m<2

Trường hợp 2: m=2

Pt sẽ là 1=0(vô lý)

Trường hợp 3: m=-2

=>-4x²+1=0(nhận)

Vậy: -2<=m<2

Đúng(1)

PT

Pham Trong Bach

5 tháng 6 2019

Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ? A. m > - 1 B. - 1 ≤ m ≤ 3 C. - 1 < m ≤ 3 D. - 1 < m < 3 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

5 tháng 6 2019

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP