Hình thoi ABCD có AB = 8cm, ÂDC = 1200 . Từ B kẻ BE ⊥ AD (E thuộc AD) , BF ⊥ DC (F thuộc CD) a) Tính các góc của hình thoi. b) Tính độ dài AE,DF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
19 tháng 7 2021
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ADC$:
$\frac{1}{DE^2}=\frac{1}{AD^2}+\frac{1}{DC^2}=\frac{1}{6^2}+\frac{1}{8^2}$
$\Rightarrow DE=4,8$ (cm)
Áp dụng hệ thức lượng trong tgv với tam giác $ADF$:
$AD^2=DE.DF$
$6^2=4,8.DF\Rightarrow DF=7,5$ (cm)
$EF=DF-DE=7,5-4,8=2,7$ (cm)
Tiếp tục áp dụng hệ thức lượng trong tgv $ADF$:
$AE^2=DE.DF=4,8.2,7=12,96\Rightarrow AE=3,6$ (cm)
$AF=\sqrt{AE^2+EF^2}=\sqrt{3,6^2+2,7^2}=4,5$ (cm) theo định lý Pitago
$BF=AB-AF=CD-AF=8-4,5=3,5$ (cm)
Áp dụng htl trong tgv với tam giác $ADC$:
$DE^2=AE.CE$
$4,8^2=3,6.CE\Rightarrow CE=6,4$ (cm)
CM
17 tháng 10 2018
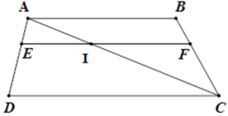
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
B F B C = A I A C = A E A D = 4 12 = 1 3 nên BF = 1 3 .BC = 1 3 .15 = 5 (cm)
Đáp án: B
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 8 2021
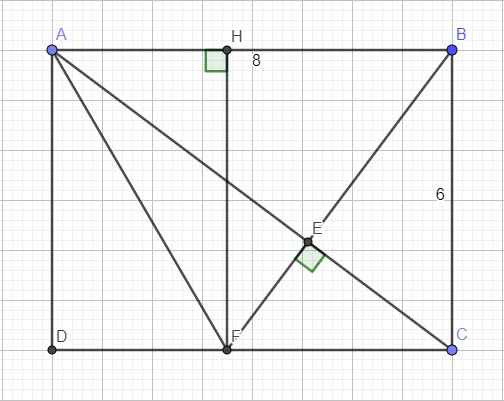
Áp dụng định lý Pitago cho tam giác vuông ABC
\(AC=\sqrt{AB^2+BC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC với đường cao BE:
\(AB^2=AE.AC\Rightarrow AE=\dfrac{AB^2}{AC}=6,4\left(cm\right)\)
\(AB.AC=BE.AC\Rightarrow AE=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\)
b.
Ta có: \(EC=AC-AE=3,6\left(cm\right)\)
Do AB song song CF, theo định lý Talet:
\(\dfrac{CF}{AB}=\dfrac{CE}{AE}\Rightarrow CF=\dfrac{AB.CE}{AE}=4,5\left(cm\right)\)
\(\Rightarrow DF=DC-CF=8-4,5=3,5\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông ADF:
\(AF=\sqrt{AD^2+DF^2}=\dfrac{\sqrt{193}}{2}\left(cm\right)\)
Pitago tam giác vuông BCF:
\(BF=\sqrt{BC^2+CF^2}=7,5\left(cm\right)\)
Kẻ FH vuông góc AB \(\Rightarrow ADFH\) là hình chữ nhật (tứ giác 3 góc vuông)
\(\Rightarrow FH=AD=6\left(cm\right)\)
\(S_{ABF}=\dfrac{1}{2}FH.AB=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
