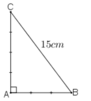
Cho tam giác ABC vuông tại A có BC = 15cm, B ^ = 55 0 . Tính AC; C ^ (làm tròn đến chữ số thập phân thứ hai)
A. A C ≈ 12 , 29 ; C ^ = 45 0
B. A C ≈ 12 , 29 ; C ^ = 35 0
C. A C ≈ 12 , 2 ; C ^ = 35 0
D. A C ≈ 12 , 92 ; C ^ = 40 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình làm mẫu cho bạn câu a) nhé
a) Theo định lí Pytago ta có :
BC2 = AB2 + AC2
152 = AB2 + AC2
AB : AC = 3:4
=> \(\frac{AB}{3}=\frac{AC}{4}\)=> \(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}\)và AB2 + AC2 = 152
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}=\frac{AB^2+AC^2}{3^2+4^2}=\frac{15^2}{25}=\frac{225}{25}=9\)
\(\frac{AB^2}{3^2}=9\Rightarrow AB^2=81\Rightarrow AB=\sqrt{81}=9cm\)
\(\frac{AC^2}{4^2}=9\Rightarrow AC^2=144\Rightarrow AC=\sqrt{144}=12cm\)
Ý b) tương tự nhé

Hình đơn giản nên tự vẽ nhá.
a) Áp dụng định lý Py-ta-go vào tam giác vuông ABC:
AC^2 + AB^2 = BC^2
=> AC^2 = BC^2 - AB^2 = 15^2 - 9^2 = 225 - 81 = 144
=> AC = căn 144 = 12 (cm)
b) Xét tam giác BIA và tam giác BIH:
BAI^ = BHI^ = 90o
IBA^ = IBH^
BI chung
=> tam giác BIA = tam giác BIH (cạnh huyền_góc nhọn)
=> BA = BH (2 cạnh tương ứng)
=> Tam giác AHB cân
a.Ta có: AB=9cm ; BC=15cm
Theo định lý Py-ta-go: BC2 = AB2 +AC2
=>AC2 =BC2 - AB2 =152 - 92 = 225-81= 144
AC2 = 144 =>AC=\(\sqrt{144}\)=12cm
b.Ta có: IH vuông góc BC tại H => tam giác BIH vuông tại H
Góc A vuông ( tam giác ABC vuông tại A ) => tsm giác ABI vuông tại A
Xét tg BIH và tg ABI có:
=> BIH = ABI ( cạnh huyền - góc nhọn)
Do đó: AB = BH
mà đây là 2 cạnh bên của tam giác ABH => ABH cân tại H

Đề 1:
a: Xét ΔABH vuông tại H có
\(AB^2=AH^2+HB^2\)
hay HB=18(cm)
Xét ΔBCA vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AH^2=HB\cdot HC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BC=50\left(cm\right)\\HC=32\left(cm\right)\end{matrix}\right.\)
Xét ΔACH vuông tại H có
\(AC^2=AH^2+HC^2\)
nên AC=40(cm)
b: Xét ΔAHC vuông tại H và ΔDHB vuông tại H có
\(\widehat{HAC}=\widehat{HDB}\)
Do đó: ΔAHC\(\sim\)ΔDHB
Suy ra: \(\dfrac{AC}{DB}=\dfrac{HC}{HB}\)
hay \(DB=\dfrac{32}{18}\cdot40=\dfrac{640}{9}\left(cm\right)\)

a: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
AH=15*20/25=12cm
BH=15^2/25=9cm
CH=25-9=16cm
b: Xet ΔABC vuông tại A và ΔDHC vuông tại D có
góc C chung
=>ΔABC đồng dạng với ΔDHC
c: \(\dfrac{S_{ABC}}{S_{DHC}}=\left(\dfrac{BC}{HC}\right)^2=\left(\dfrac{25}{16}\right)^2\)
=>\(S_{DHC}=150:\dfrac{625}{256}=61.44\left(cm^2\right)\)

Theo đề bài ta có:
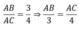
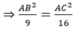
Theo tính chất dãy tỉ số bằng mhau ta có:
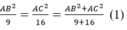
tam giác ABC vuông tại A
Áp dụng định lí pitago vào tam giác ABC ta có:
BC2 = AB2 + AC2 (2)
Từ (1) và (2) suy ra:
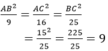
AB2 = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)
AC2 = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)

a: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc MAC+góc AED=90 độ
=>góc MAC+góc AHD=90 độ
=>góc MAC+góc B=90 độ
=>góc MAC=góc MCA và góc MAB=góc MBA
=>MA=MB=MC
=>M là trung điểm của BC
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=20^2/25=16(cm)
AD=12^2/15=144/15=9,6cm
AE=12^2/20=7,2cm
\(S_{ADE}=\dfrac{1}{2}\cdot7.2\cdot9.6=34.56\left(cm^2\right)\)
Xét tam giác ABC vuông tại A có:
Đáp án cần chọn là: B