Tìm các số nguyên tố x,y sao cho : x2-2y2=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
\(\Leftrightarrow x^2-1=2y^2\)
Do vế phải chẵn \(\Rightarrow\) vế trái chẵn \(\Leftrightarrow x\) lẻ
\(\Rightarrow x=2k+1\)
Pt trở thành: \(\left(2k+1\right)^2-1=2y^2\Leftrightarrow2\left(k^2+k\right)=y^2\)
Vế trái chẵn \(\Rightarrow\) vế phải chẵn \(\Rightarrow y^2\) chẵn \(\Rightarrow y\) chẵn
\(\Rightarrow y=2\)
\(\Rightarrow x^2-9=0\Rightarrow x=3\)
Vậy \(\left(x;y\right)=\left(3;2\right)\)
NP
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2021
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2z+1\right)< 1\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-1\right)^2< 1\)
Nếu tồn tại 1 trong 3 số \(x-y;y-z;z-1\) khác 0
Do x; y; z nguyên
\(\Rightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge1\) (vô lý)
\(\Rightarrow x-y=y-z=z-1=0\)
\(\Leftrightarrow x=y=z=1\)
OY
10 tháng 8 2021
Ta có: x:y:z =4:5:6
⇒\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}\)
⇒\(\dfrac{x^2}{16}=\dfrac{2y^2}{50}=\dfrac{z^2}{36}\)
⇒\(\dfrac{x^2-2y^2+z^2}{16-50+36}=\dfrac{18}{2}=9\)
\(\dfrac{x}{4}=9\Rightarrow x=36\)
\(\dfrac{y}{5}=9\Rightarrow y=45\)
\(\dfrac{z}{6}=9\Rightarrow z=54\)
NT
0
BN
3
18 tháng 2 2016
Với x = 2, ta có: 22 + 117 = y2 → y2 = 121 → y = 11 (là số nguyên tố)
* Với x > 2, mà x là số nguyên tố nên x lẻ y2 = x2 + 117 là số chẵn
=> y là số chẵn
kết hợp với y là số nguyên tố nên y = 2 (loại)
Vậy x = 2; y = 11.
c. Ta có: 1030= 100010 và 2100 =102410. Suy ra: 1030 Lại có: 2100= 231.263.26 = 231.5127.64 và 1031=231.528.53=231.6257.125
Nên: 2100
18 tháng 2 2016
117=(y+x)(y-x)=3.39=39.3=9.13=13.9
Ta cá bảng
| x-y | 3 | 39 | 9 | 13 |
| x+y | 39 | 3 | 13 | 9 |
| x | 21 | 21 | 11 | 11 |
| y | 18 | -18 | 2 | -2 |
chỉ có x=11 và y=2 là số nguyên tố
vậy ....
vì 2y2\( {\vdots}\)2 nên (x-1)(x+1)\( {\vdots}\)2
vì x-1+x+1=2x
x-1 và x+1 có cùng tính chẵn lẻ
Và từ y=2 ta thay vào x2-2y2=1
x2-2.22=1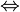 
x2 = 9 
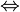x = 3
Vật số nguyên tố (x, y) là cặp số (3, 2)