Cho tam giác ABC có D là trung điểm của BC. Điểm E thuộc đoạn CD sao cho CE=2DE và \(\widehat{CAE}=\widehat{DAE}\). Chứng minh tam giác ABC vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thế Việt
VIP
24 tháng 2 2022
lkjhgfgy6tyur65445676t 7 777676r64576556756777777777777/.,mnbvfggjhyjuhjtyj324345
27 tháng 8 2022
Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
13 tháng 4 2022
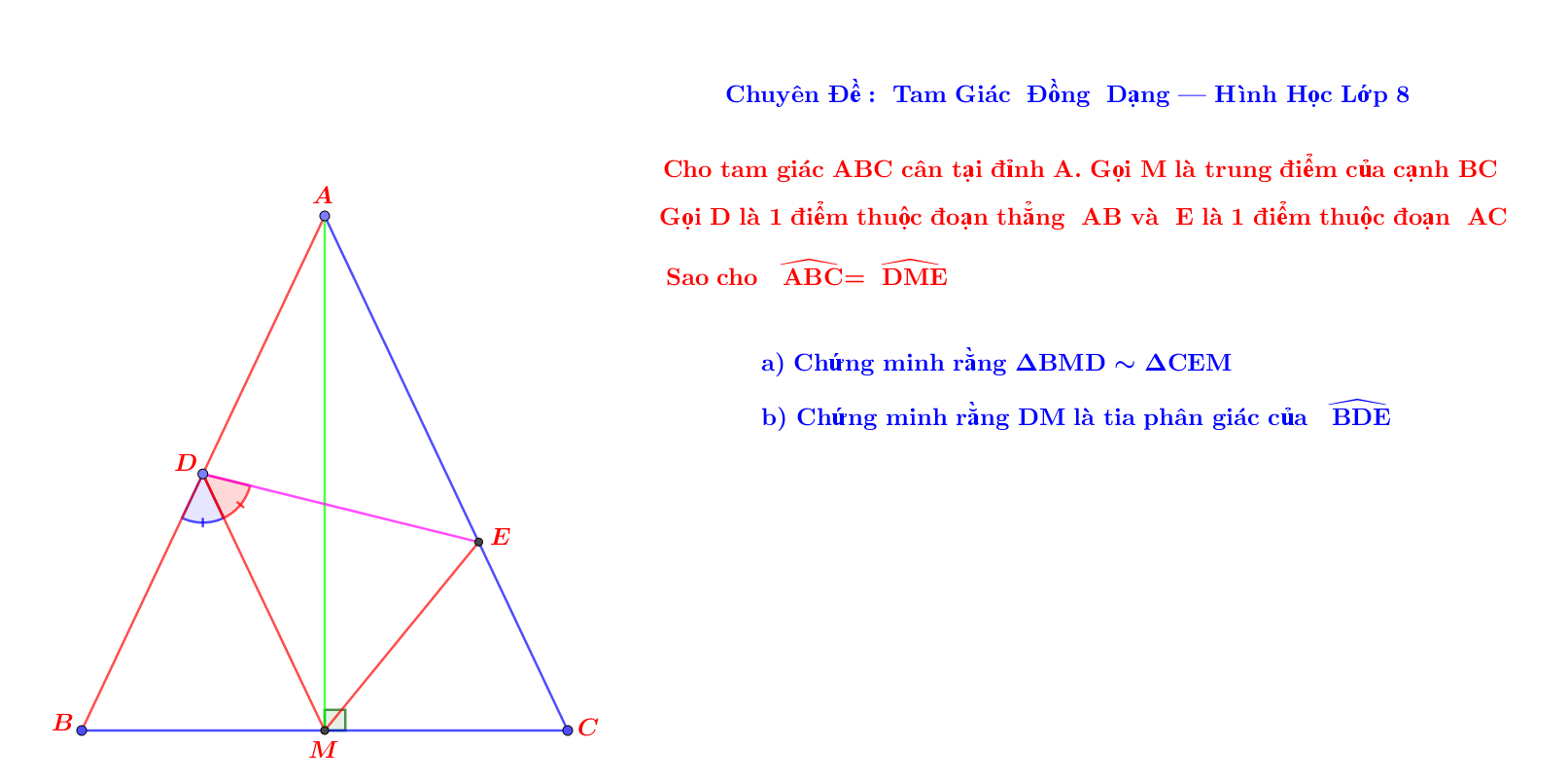
a) \(\widehat{BDM}=180^0-\widehat{BMD}-\widehat{DBM}=180^0-\widehat{BMD}-\widehat{DME}=\widehat{CME}\)
\(\Rightarrow\)△BMD∼△CEM (g-g)
b) \(\Rightarrow\dfrac{BD}{CM}=\dfrac{MD}{EM}\Rightarrow\dfrac{BD}{BM}=\dfrac{MD}{EM}\)
\(\Rightarrow\)△BMD∼△MED (c-g-c).
\(\Rightarrow\widehat{BDM}=\widehat{MDE}\Rightarrow\)DM là tia p/g góc BDE.
27 tháng 2 2019
cau 1 :
Xet tam giac ABD va tam giac EBD co : BD chung
goc ABD = goc DBE do BD la phan giac cua goc ABC (gt)
AB = BE (Gt)
=> tam giac ABD = tam giac EBD (c - g - c)
=> goc BAC = goc DEB (dn)
ma goc BAC = 90 do tam giac ABC vuong tai A (gt)
=> goc DEB = 90
=> DE _|_ BC (dn)
b, tam giac ABD = tam giac EBD (cau a)
=> AB = DE (dn)
AB = 6 (cm) => DE = 6 cm
DE _|_ BC => tam giac DEC vuong tai E
=> DC2 = DE2 + CE2 ; DC = 10 cm (gt); DE = 6 cm (cmt)
=> CE2 = 102 - 62
=> CE2 = 64
=> CE = 8 do CE > 0
