1/trong không gian với hệ tọa độ oxyz, cho tọa độ các điểm A(1;2;3),B(2;-1;0),C(0;1;-1). Diện tích tam giác ABC là
A/\(\frac{\sqrt{166}}{2}\) B/\(\frac{\sqrt{156}}{2}\) C\(\frac{\sqrt{146}}{2}\) D \(\frac{\sqrt{146}}{3}\)
2.trong khong gian oxyz, cho điểm A(4;-3;2) và đường thẳng (d)\(^{\frac{x+2}{3}}=\frac{y+2}{2}=\frac{z}{-1}\). Tọa độ hình chiểu vuông góc của A lên đường thẳng d là
A H(1;0;-1) B(-1;0;-1) C H(0;1;-1) D H(-1;0;1)
3 Nguyên hàm F(X) của hàm số f(x)=3x^5(2-3x), biết F(-1)=1 là




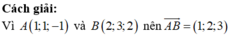

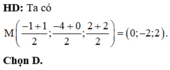
1.
\(\overrightarrow{AB}=\left(1;-3;-3\right);\overrightarrow{AC}=\left(-1;-1;-4\right)\)
\(\Rightarrow\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(9;7;-4\right)\)
\(\Rightarrow S_{ABC}=\frac{1}{2}\left|\left[\overrightarrow{AB};\overrightarrow{AC}\right]\right|=\frac{1}{2}\sqrt{9^2+7^2+4^2}=\frac{\sqrt{146}}{2}\)
2.
Phương trình mặt phẳng (P) qua A và vuông góc d là:
\(3\left(x-4\right)+2\left(y+3\right)-1\left(z-2\right)=0\)
\(\Leftrightarrow3x+2y-z-4=0\)
Tọa độ H là nghiệm: \(\left\{{}\begin{matrix}\frac{x+2}{3}=\frac{y+2}{2}=\frac{z}{-1}\\3x+2y-z-4=0\end{matrix}\right.\) \(\Rightarrow H\left(1;0;-1\right)\)
3.
\(f\left(x\right)=6x^5-9x^6\)
\(\Rightarrow F\left(x\right)=\int\left(6x^5-9x^6\right)dx=x^6-\frac{9}{7}x^7+C\)
\(F\left(-1\right)=1\Leftrightarrow1+\frac{9}{7}+C=1\Rightarrow C=-\frac{9}{7}\)
\(\Rightarrow F\left(x\right)=-\frac{9}{7}x^7+x^6-\frac{9}{7}\)

\n