Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp
+) Gọi I là điểm thỏa mãn hệ thức I A → + I B → + 3 I C → = 0 → tìm tọa độ điểm I.
+) Chứng minh M A 2 + M B 2 + 3 M C 2 nhỏ nhất <=> MI nhỏ nhất.
+) MI nhỏ nhất <=> M là hình chiếu của I trên (P)
Cách giải
Gọi là điểm thỏa mãn ta có hệ phương trình:

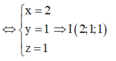
Ta có:
![]()
![]()
![]()
![]()
![]()
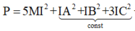

![]()
Khi đó M là hình chiếu của I trên (P)
Gọi d là đường thẳng đi qua I và vuông góc với (P)

![]()
M ∈ (P) Suy ra
=> 3(3t+2) - 3(-3t+1)-2(-2t+1)-12=0
=> a+ b+ c =3

Đáp án D
Phương pháp giải:
Xác định tọa độ hình chiếu trên mặt phẳng và lấy trung điểm ra tọa độ điểm đối xứng
Lời giải:
Hình chiếu của A(2;1;-3) trên mặt phẳng (Oyz) là H(0;1;-3)
Mà H là trung điểm của AA' suy ra tọa độ điểm A'(-2;1;-3)

Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).
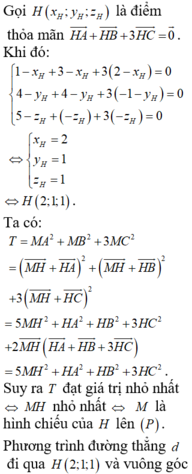

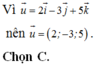

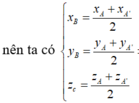
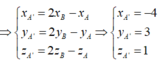

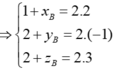
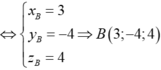
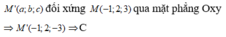
Đáp án D
Dễ thấy phương trình mặt phẳng (Oxz): y = 0 nên suy ra điểm đối xứng với A(1; -4; - 5) qua (Oxz) là điểm A'(1;4;-5).