Bài 1: Cho Δ ABC có AB = 8cm,AC = 6cm,BC = 10cm. Tam giác A'B'C' đồng dạng với tam giác ABC có độ dài cạnh lớn nhất là 25 cm. Tính độ dài các cạnh còn lại của Δ A'B'C' ?
Bài 2 : Cho Δ ABC ∼ Δ DEF có tỉ số đồng dạng là k = 3/5, chu vi của Δ ABC bằng 12cm. Chu vi của Δ DEF là?

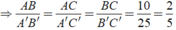
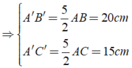
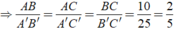
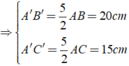

Bài 1:
Ta có: ΔA'B'C'\(\sim\)ΔABC(gt)
⇔\(\frac{A'B'}{AB}=\frac{A'C'}{AC}=\frac{B'C'}{BC}=k\)
hay \(\frac{A'B'}{8}=\frac{A'C'}{6}=\frac{B'C'}{10}\)
⇔B'C'>A'B'>A'C'
hay B'C' là cạnh lớn nhất trong ΔA'B'C'
mà độ dài cạnh lớn nhất là 25cm
nên B'C'=25cm
⇔\(\frac{A'B'}{8}=\frac{A'C'}{6}=\frac{25}{10}\)
\(\Leftrightarrow\left\{{}\begin{matrix}A'B'=\frac{8\cdot25}{10}=\frac{200}{10}=20cm\\A'C'=\frac{25\cdot6}{10}=\frac{150}{10}=15cm\end{matrix}\right.\)
Vậy: A'B'=20cm; A'C'=15cm
Bài 2:
Ta có: ΔABC\(\sim\)ΔDEF với tỉ số đồng dạng \(k=\frac{3}{5}\)
⇔\(\frac{C_{ABC}}{C_{DEF}}=\frac{3}{5}\)
hay \(C_{DEF}=\frac{5\cdot12}{3}=\frac{60}{3}=20cm\)
Vậy: Chu vi của ΔDEF là 20cm
cảm ơn bạn