Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{AD}{AB}=\dfrac{CD}{BC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{AD}{6}=\dfrac{CD}{10}\)
mà AD+CD=AC(D nằm giữa A và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{CD}{10}=\dfrac{AD+CD}{6+10}=\dfrac{AC}{16}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{AD}{6}=\dfrac{1}{2}\\\dfrac{CD}{10}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AD=3\left(cm\right)\\CD=5\left(cm\right)\end{matrix}\right.\)
Vậy: BC=10cm; AD=3cm; CD=5cm
b) Ta có: \(\dfrac{CE}{CA}=\dfrac{4}{8}=\dfrac{1}{2}\)
\(\dfrac{CD}{CB}=\dfrac{5}{10}=\dfrac{1}{2}\)
Do đó: \(\dfrac{CE}{CA}=\dfrac{CD}{CB}\)
Xét ΔCED và ΔCAB có
\(\dfrac{CE}{CA}=\dfrac{CD}{CB}\)(cmt)
\(\widehat{C}\) chung
Do đó: ΔCED\(\sim\)ΔCAB(c-g-c)

a: BC=10cm
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔHAB∼ΔHCA

Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(=\dfrac{1}{4}\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
Xét ΔABC có MN//BC(cmt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow MN=\dfrac{1}{4}\cdot8=2\left(cm\right)\)

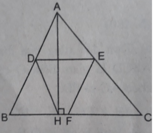
S D E C H = 22 c m 2 ; S B D E F = 20 c m 2 ; S D E F H = 12 c m 2

TK
Vậy AB = 4cm, BC = 8cm, AC = 6cm
Đáp án cần chọn là: C
C