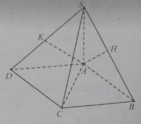
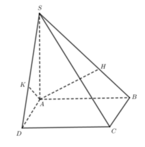
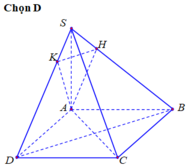
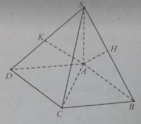
Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với mặt đáy . Dựng AH , AK , AM lần lượt là các đường cao trong các tam giác SAB , SAD , SAC
1)CMR: AH vuông góc với SC , AK vuông góc với SC . Chứng tỏ AH , AK , AM đồng phẳng
2)CMR: KH vuông góc với AM



\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\)
\(BC\perp AB\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\) (1)
Hoàn toàn tương tự ta có \(AK\perp\left(SCD\right)\Rightarrow AK\perp SC\) (2)
(1);(2) \(\Rightarrow SC\perp\left(AHK\right)\)
Mà \(SC\perp AM\) ; \(A\in\left(AHK\right)\Rightarrow AM\in\left(AHK\right)\)
\(\Rightarrow AH;AK;AM\) cùng thuộc mặt phẳng (AHK) là mp vuông góc SC
b/ Áp dụng hệ thức lượng:
\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AB^2};\) \(\frac{1}{AK^2}=\frac{1}{SA^2}+\frac{1}{AD^2}\)
Mà AB=AD \(\Rightarrow AH=AK\Rightarrow\Delta AHK\) cân tại A
\(AH\perp\left(SBC\right)\Rightarrow AH\perp HM\Rightarrow\Delta AHM\) vuông tại H
Tương tự \(\Delta AKM\) vuông tại K
Xét 2 tam giác vuông \(AHM\) và \(AKM\) có: AM chung, AH=AK (cmt)
\(\Rightarrow\Delta AHM=\Delta AKM\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{HAM}=\widehat{KAM}\Rightarrow AM\) là phân giác góc \(\widehat{HAK}\)
\(\Rightarrow AM\) đồng thời là đường cao trong tam giác AHK (do cân tại A)
\(\Rightarrow AM\perp HK\)