Cho ΔABC nhọn, đường cao AH. Vẽ các điểm D, E sao cho các đường thẳng AB, AC l ần lượt là trung trực của các đoạn thẳng HD, HE. a) Chứng minh rằng AD = AE b) Gọi M, N lần lượt là giao điểm của đường thẳng DE với AB, AC. Chứng minh rằng HA là tia phân giác của MHN c) Chứng minh rằng goc DAE=2 goc MHB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
11 tháng 8 2015
d) ta co : goc BHI+goc IHA =90 ( 2 goc ke phu)
----> goc BHI =90- goc IHA
ma goc IHA = goc ADI ( tam giac ADI = tam giac AHI)
nen goc BHI=90- goc ADI (1)
ta co :
goc ADE = (180- goc DAE):2 ( tam giac ADE can tai A)
ma goc DAE= 2. goc BAC ( cm cau b)
nen goc ADE = (180-2.goc BAC):2= 90-goc BAC
---> goc BAC =90- goc ADE (2)
tu (1) va (2) suy ra goc BHI= goc BAC
23 tháng 5 2016
Cho tam giác ABC nhọn, đường cao AH. Vẽ điểm D và E sao cho các đường thẳng AB, Ac lad các đường trung trực của DH và EH. Lấy điểm M, N lần lượt là giao điểm của DE với AB và Ac
a) Chứng minh AB= Ae
b)Chứng minh góc DAE bằng 2 lần góc MHB
c)Chứng minh AH, BN, CM đồng quy tại 1 điểm
13 tháng 4 2017
làm ơn giúp mk đi mấy bạn ( dặc biệt là @Nguyễn Huy Tú, @Ace Legona, @soyeon_Tiểubàng giải, @Trần Việt Linh, @Hoàng Lê Bảo Ngọc, @Võ Đông Anh Tuấn nha)
TG
14 tháng 7 2020
a) Gọi I và K lần lượt là giao điểm của DH và AB; HE và AC
Xét 2 tam giác vuông ΔAID và ΔAIH ta có:
AI: cạnh chung
DI = HI (GT)
=> ΔAID = ΔAIH (c.g.v - c.g.v)
=> AD = AH (2 cạnh tương ứng) (1)
Xét 2 tam giác vuông ΔAKH và ΔAKE:
HK = EK (GT)
AK: cạnh chung
=> ΔAKH = ΔAKE (c.g.v - c.g.v)
=> AH = AE (2 cạnh tương ứng) (2)
Từ (1) và (2) => AD = AE
b) AD = AE (cmt)
=> Tam giác ADE cân tại A
\(\Rightarrow\widehat{ADE}=\widehat{AED}\) (3)
Ta có: M ∈ AB
=> M ∈ đường trung trực của DH
=> MD = MH
Xét ΔAMD và ΔAMH ta có:
AD = AH (cmt)
MD = MH (cmt)
AM: cạnh chung
=> ΔAMD = ΔAMH (c - c - c)
\(\Rightarrow\widehat{ADM}=\widehat{AHM}\) (2 góc tương ứng)
Hay: \(\widehat{ADE}=\widehat{AHM}\) (4)
Ta có: N ∈ đường trung trực của HE
=> HN = EN
Xét ΔAHN và ΔAEN ta có:
HN = EN (cmt)
AH = AE (cmt)
AN: cạnh chung
=> ΔAHN = ΔAEN (c - c - c)
\(\Rightarrow\widehat{AHN}=\widehat{AEN}\) (2 góc tương ứng)
Hay: \(\widehat{AHN}=\widehat{AED}\left(5\right)\)
Từ (3); (4) và (5) \(\Rightarrow\widehat{AHM}=\widehat{ADE}=\widehat{AED}=\widehat{AHN}\)
Hay: \(\widehat{AHM}=\widehat{AHN}\)
=> AH là phân giác của góc MHN
P/s: Mấy câu còn lại khó quá chưa nghĩ ra!
CM
28 tháng 10 2017
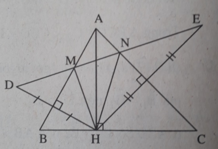
M thuộc đường trung trực của HD nên MH = MD. MB là đường trung trực của đáy HD của tam giác cân HMD nên MB là tia phân giác của góc HMD. Tương tự NC là tia phân giác của góc HNE. Vậy MB, NC là các đường phân giác góc ngoài của ΔHMN.
Các đường thẳng MB, NC cắt nhau tại A nên HA là đường phân giác trong của góc MHN của ΔHMN.
+) HC vuông góc với HA tại H mà HA là đường phân giác trong của góc MHN nên HC là đường phân giác góc ngoài của ΔHMN.( đường phân giác góc trong và góc ngoài tại 1 đỉnh của 1 tam giác vuông góc với nhau)
+) Các đường thẳng HC và NC cắt nhau tại C; HC và NC là hai đường phân giác ngoài của tam giác HMN nên MC là đường phân giác góc trong của ΔHMN.
MB và MC là các tia phân giác của hai góc kề bù ∠DMH; ∠HMA nên MB ⊥ MC.
Vậy MC ⊥ AB.
