nhìn vào hình 3, chứng minh tam giác BEM đồng dạng với tam giác CMF biết tam giác ABC là tam giác đều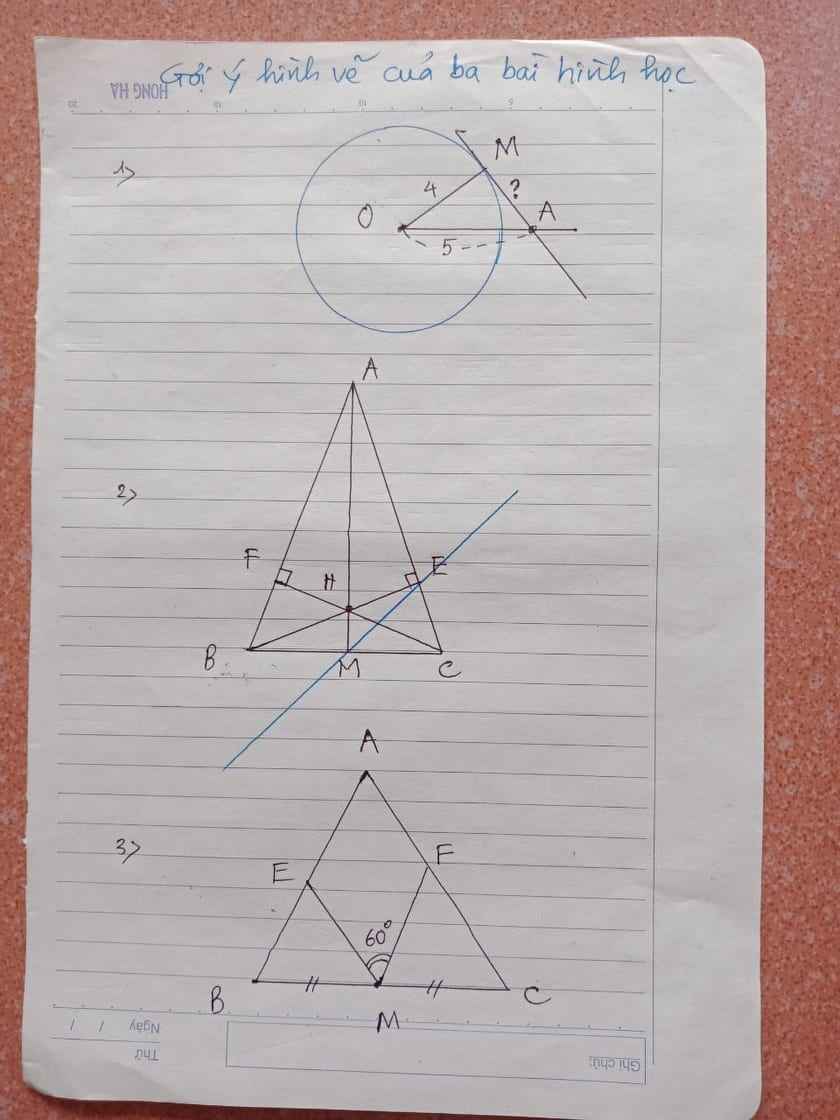
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 2 2015
a/ Xét tam giác BEM và tam giác CMF có:
góc BEM = góc CFM = 900
BM = MC (M là trung điểm của BC)
góc BME = góc CMF (đối đỉnh)
Do đó: tam giác BEM = tam giác CMF (cạnh huyền - góc nhọn)
Vậy: tam giác BEM = tam giác CMF.
b/ Ta có:
BE vuông góc với AM, CF vuông góc với AM => BE// CF
Vậy: BE//CF
c/ Ta có:
tam giác BEM = tam giác CMF (cmt) =>ME = MF
=> M là trung điểm của EF
Vậy: M là trung điểm của EF
(mấy kí hiệu bạn tự viết nha)
26 tháng 3 2016
Mình đã giải xong câu a, b, c. Nhờ các bạn và quý thầy cô giải giúp câu d. Chỉ cần tóm tắt lời giải thôi cũng được ạ.
HS
26 tháng 3 2016
d) SADE = 1/2.AD.AE ; SABC = 1/2.AB.AC => SADE / SABC = AD.AE/AB.AC =1/4 (1)
Do tg ADE đồng dạng tg ABC => SADE / SABC = (DE/BC)2 = (AH/BC)2 (2)
Từ (1) và (2) => AH/BC = 1/2 hay AH = !/2 BC. Vậy AH là đường trung tuyến tg ABC, mà AH là đường cao => tg ABC cân tại A
7 tháng 4 2022
a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: \(\dfrac{S_{ABC}}{S_{HBA}}=\dfrac{25}{9}\)
nên \(S_{HBA}=24:\dfrac{25}{9}=24\cdot\dfrac{9}{25}=8.64\left(cm^2\right)\)
23 tháng 3 2016
Gọi D, E và F theo thứ tự là trung điểm các cạnh BC, CA và AB của tam giác ABC. Ta có :
\(\overrightarrow{AB'}=\overrightarrow{AE}+\overrightarrow{EB'}=\frac{1}{2}\overrightarrow{c}+\overrightarrow{EB'}\)
\(\overrightarrow{AC'}=\overrightarrow{AF}+\overrightarrow{FC'}=\frac{1}{2}\overrightarrow{b}+\overrightarrow{FC'}\)
\(\overrightarrow{AA'}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DA'}=\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}+\overrightarrow{DA}\)
Do đó, điều phải chứng minh tương đương với
\(\overrightarrow{AB'}=\overrightarrow{FC'}=\overrightarrow{DA'}\)
Giả sử tam giác ABC định hướng dương. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{2}\) và
\(k=\cot\widehat{B'AC}=\cot\widehat{C'AB}\)
Ta có
\(f\left(\overrightarrow{EB'}+\overrightarrow{FC'}\right)=f\left(\overrightarrow{EB'}\right)+f\left(\overrightarrow{FC'}\right)\)
\(=k\overrightarrow{EA}+k\overrightarrow{AF}=\frac{k}{2}\left(\overrightarrow{b}-\overrightarrow{c}\right)\) (do \(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}=0\) )
\(=\frac{k}{2}\overrightarrow{CB}=k\overrightarrow{DB}=f\left(\overrightarrow{DA'}\right)\)
Suy ra điều cần chứng minh
DL
1 tháng 5 2018
a, tam giac AHE và ABH có:
BAH là góc chung
góc AEH = AHB = 90
Nên tg AHE đồg dag vs tg ABH (g.g)
b, Áp dụng định lí Py-ta-go vào tam giac vuông AHB và AHC tính dc BH và CH
=> BC = BH +CH
c, AHE đồng dạng ABH (theo a) => AE/AH = AH/AB => AE.AB = AH^2 (1)
Tương tự: AHF đồg dag ACH (g.g) => AF/AH = AH/AC => AF.AC = AH^2 (2)
Từ (1) và (2) => AE.AB = AF.AC => AE/AF = AC/AB
=> AFE đồng dạng ABC (c.g.c)
28 tháng 3 2023
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc A chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AB*AF=AE*AC: AB/AE=AC/AF
b: Xet ΔABC và ΔAEF có
AB/AE=AC/AF
góc BAC chung
=>ΔABC đồng dạng với ΔAEF
góc BFC=góc BDA=90 độ
mà góc B chung
nên ΔBFC đồng dạng với ΔBDA
=>BF/BD=BC/BA
=>BF/BC=BD/BA
=>ΔBFD đồng dạng với ΔBCA
ΔABC đều ⇒\(\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
\(\widehat{B}=\widehat{EMF}=60^o\) mà 2 góc này là 2 góc SLT ⇒AB//FM⇒AE//FM (1)
\(\widehat{C}=\widehat{EMF}=60^o\)mà 2 góc này là 2 góc SLT ⇒AC//EM⇒AF//EM (2)
Từ (1) và (2) ⇒ AEMF là hbh
\(\Rightarrow\widehat{AEM}=\widehat{AFM}\Rightarrow\widehat{BEM}=\widehat{CFM}\) (kề bù với 2 góc bằng nhau)
Xét Δ BEM và ΔCMF có:
\(\widehat{B}=\widehat{C}\left(=60^o\right)\)
\(\widehat{BEM}=\widehat{CFM}\) (chứng minh trên)\
⇒Δ BEM ∼ ΔCMF(g.g)