Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Xét ADB và tam giác AEC ta có:
`hat{AEC}=hat{ADB}=90^o`(gt)
`hat{A}` chung
`=>Delta ADB~Delta AEC(gg)`
b)Vì `Delta ADB~Delta AEC(gg)`
`=>(AB)/(AC)=(AE)/(AD)`
`=>DeltaADE~Delta ABC(cgc)`
c)
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{A}\) chung
Do đó: ΔADB∼ΔAEC(g-g)
b) Ta có: ΔADB∼ΔAEC(cmt)
nên \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔADE∼ΔABC(c-g-c)

Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
Xét ΔAHB vuông tại H và ΔACD vuông tại C có
\(\widehat{ABH}=\widehat{ADC}\)
Do đó: ΔAHB∼ΔACD

b: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE\(\sim\)ΔACB
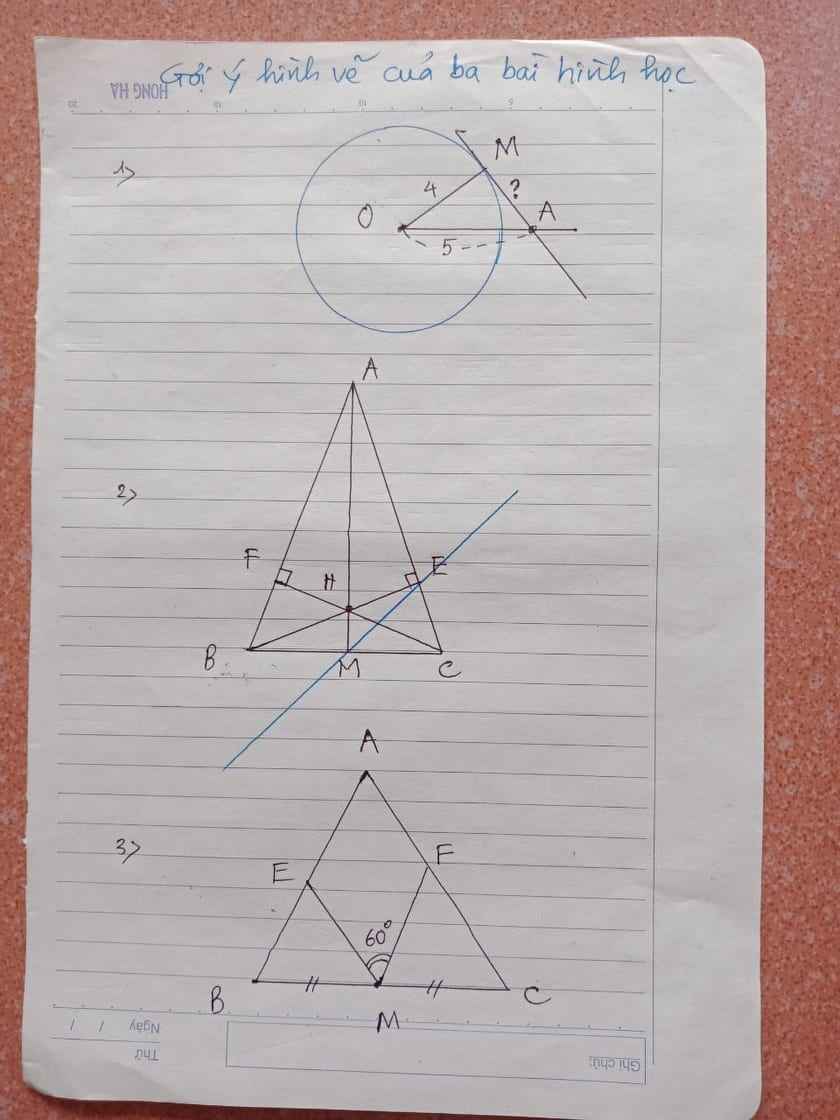
ΔABC đều ⇒\(\widehat{A}=\widehat{B}=\widehat{C}=60^o\)
\(\widehat{B}=\widehat{EMF}=60^o\) mà 2 góc này là 2 góc SLT ⇒AB//FM⇒AE//FM (1)
\(\widehat{C}=\widehat{EMF}=60^o\)mà 2 góc này là 2 góc SLT ⇒AC//EM⇒AF//EM (2)
Từ (1) và (2) ⇒ AEMF là hbh
\(\Rightarrow\widehat{AEM}=\widehat{AFM}\Rightarrow\widehat{BEM}=\widehat{CFM}\) (kề bù với 2 góc bằng nhau)
Xét Δ BEM và ΔCMF có:
\(\widehat{B}=\widehat{C}\left(=60^o\right)\)
\(\widehat{BEM}=\widehat{CFM}\) (chứng minh trên)\
⇒Δ BEM ∼ ΔCMF(g.g)