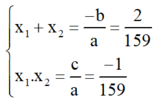1 giải phương trình sau
a) x^2 -13x +36 =0
b) x^2 -8x +9=0
2/ tìm 2 số biết tổng của chúng là 1 và tích là -20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: \(\Leftrightarrow4x^2\left(ax-3\right)-\left(ax-3\right)=0\)
\(\Leftrightarrow\left(ax-3\right)\left(2x-1\right)\left(2x+1\right)=0\)
Trường hợp 1: a=0
=>(2x-1)(2x+1)=0
=>x=1/2 hoặc x=-1/2
Trường hợp 2: a<>0
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\\x=\dfrac{3}{a}\end{matrix}\right.\)
b: \(\Leftrightarrow a^2x^2\left(2x+5\right)-4\left(2x+5\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(a^2x^2-4\right)=0\)
Trường hợp 1: a=0
Phương trình sẽ là 2x+5=0
hay x=-5/2
Trường hợp 2: a<>0
Phương trình sẽ là \(\left(2x+5\right)\left[\left(ax\right)^2-4\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=-\dfrac{2}{a}\\x=\dfrac{2}{a}\end{matrix}\right.\)

Ta có \(x^2+9x+20=0\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=-5\end{matrix}\right.\).
Xét 2 TH:
+) a + b = -4; ab = -5: Theo định lý Viet đảo ta có a, b là hai nghiệm của pt \(t^2+4t-5=0\Leftrightarrow\left(t-1\right)\left(t+5\right)=0\Leftrightarrow\left[{}\begin{matrix}t=1\\t=-5\end{matrix}\right.\)
+) a + b = -5; ab = -4: Bạn giải tương tự.

Bài 1:
a) \(\Rightarrow3x^2+3x-2x^2-4x+x+1=0\)
\(\Rightarrow x^2=-1\left(VLý\right)\Rightarrow S=\varnothing\)
b) \(\Rightarrow\left(x-2020\right)\left(2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2020\\x=\dfrac{1}{2}\end{matrix}\right.\)
c) \(\Rightarrow\left(x-10\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)
d) \(\Rightarrow\left(x+4\right)^2=0\Rightarrow x=-4\)
e) \(\Rightarrow\left(x+6\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=7\end{matrix}\right.\)
f) \(\Rightarrow\left(5x-4\right)\left(5x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Bài 2:
a) \(\Rightarrow3x\left(x^2-4\right)=0\Rightarrow3x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)

3:
a: u+v=14 và uv=40
=>u,v là nghiệm của pt là x^2-14x+40=0
=>x=4 hoặc x=10
=>(u,v)=(4;10) hoặc (u,v)=(10;4)
b: u+v=-7 và uv=12
=>u,v là các nghiệm của pt:
x^2+7x+12=0
=>x=-3 hoặc x=-4
=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)
c; u+v=-5 và uv=-24
=>u,v là các nghiệm của phương trình:
x^2+5x-24=0
=>x=-8 hoặc x=3
=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)

1) Gọi 2 số là a và b, ta có: Tổng 2 số và tích 2 số đối nhau nên:
a + b = -ab
<=> a + b + ab = 0
<=> a + ab + b + 1 = 1
<=> a (b + 1) + (b + 1) = 1
<=> (b + 1) (a + 1) = 1
Mà 1 = 1 . 1 = (-1) . (-1) nên các trường hợp là:
a + 1 = 1 và b + 1 = 1 => a = b = 0
a + 1 = -1 và b + 1 = -1 => a = b = -2
2)a) vì 8 = 8.1 = 1.8 = 2.4 = 4.2
Vì 2y + 1 là số lẻ nên chỉ có 1 phương án là:
2y + 1 = 1 và x - 2 = 8 => y = 0 và x = 10
2b) 20 = 20 . 1 = 1 . 20 = 2.10 = 10.2 = 4.5 = 5.4
Mà 4y + 1 là số lẻ nên chỉ có thể có 2 trường hợp sau:
+) 4y + 1 = 1 và 8 - x = 20 => y = 0 và x = -12
+) 4y + 1 = 5 và 8 - x = 4 => y = 1 và x = 4
1. Gọi số cần tìm là xy (x,y thuộc Z)
Ta có: x+y=xy
=> x-xy+y=0
=> x(1-y)+y-1=-1
=> x(1-y)-(1-y)=-1
=> (x-1)(1-y)=-1
=> x-1, 1-y thuộc Ư(-1)={-1,1}
Ta có bảng sau:
| x-1 | -1 | 1 |
| 1-y | 1 | -1 |
| x | 0 | 2 |
| y | 0 | 2 |
Vậy (x,y)=(0,0);(2,2)

\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)
d: \(\Leftrightarrow3x^2-6x-2x+4=0\)
=>(x-2)(3x-2)=0
=>x=2 hoặc x=2/3
e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)
=>x(x-3)(x+1)=0
hay \(x\in\left\{0;3;-1\right\}\)
f: \(\Leftrightarrow x^2-5x-2+x=0\)
\(\Leftrightarrow x^2-4x-2=0\)
\(\Leftrightarrow\left(x-2\right)^2=6\)
hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)

Bài này mik nghĩ phải giải bằng cách lập hệ pt
Gọi số thứ nhất là a, gọi thứ 2 là b
Theo bài ra ta có:
\(\left\{{}\begin{matrix}a+b=63\\a-b=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a+b+a-b=63+9\\a-b=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2a=72\\a-b=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=36\\36-b=9\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=36\\b=27\end{matrix}\right.\)

a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 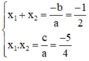
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 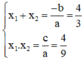
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: