Cho tam giác ABC cân tại A có AB = AC =10cm , BC = 12cm. Vẽ AH vuông góc BC tại H. a) Chứng minh ∆ABH = ∆ACH . b) Tính độ dài AH. c) Từ H vẽ HM vuông góc AB (MAB ) , vẽ HN vuông góc AC (NAC) . Chứng minh ∆BHM = ∆CHN. d) Từ B vẽ Bx vuông góc AB, từ C vẽ Cy vuông góc AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì...
Đọc tiếp
Cho tam giác ABC cân tại A có AB = AC =10cm , BC = 12cm. Vẽ AH vuông góc BC tại H. a) Chứng minh ∆ABH = ∆ACH . b) Tính độ dài AH. c) Từ H vẽ HM vuông góc AB (MAB ) , vẽ HN vuông góc AC (NAC) . Chứng minh ∆BHM = ∆CHN. d) Từ B vẽ Bx vuông góc AB, từ C vẽ Cy vuông góc AC chúng cắt nhau tại O. Tam giác OBC là tam giác gì? Vì sao?
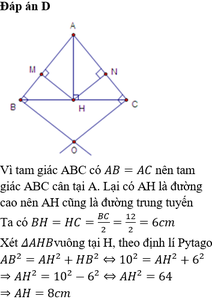
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(gt)
AH là cạnh chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
b) Ta có: ΔABH=ΔACH(cmt)
⇒BH=CH(hai cạnh tương ứng)
mà BH+CH=BC=12cm(H nằm giữa B và C)
nên \(BH=CH=\frac{BC}{2}=\frac{12}{2}=6cm\)
Áp dụng định lí pytago vào ΔABH vuông tại H, ta được
\(AB^2=AH^2+BH^2\)
hay \(AH^2=AB^2-BH^2=10^2-6^2=64\)
⇔\(AH=\sqrt{64}=8cm\)
Vậy: AH=8cm
c) Xét ΔBHM vuông tại M và ΔCHN vuông tại N có
BH=CH(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBHM=ΔCHN(cạnh huyền-góc nhọn)
d) Ta có: \(\widehat{ABC}+\widehat{OBC}=\widehat{ABO}=90^0\)(tia BC nằm giữa hai tia BA,BO)
\(\widehat{ACB}+\widehat{OCB}=\widehat{ACO}=90^0\)(tia CB nằm giữa hai tia CA,CO)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(định lí đảo của tam giác cân)