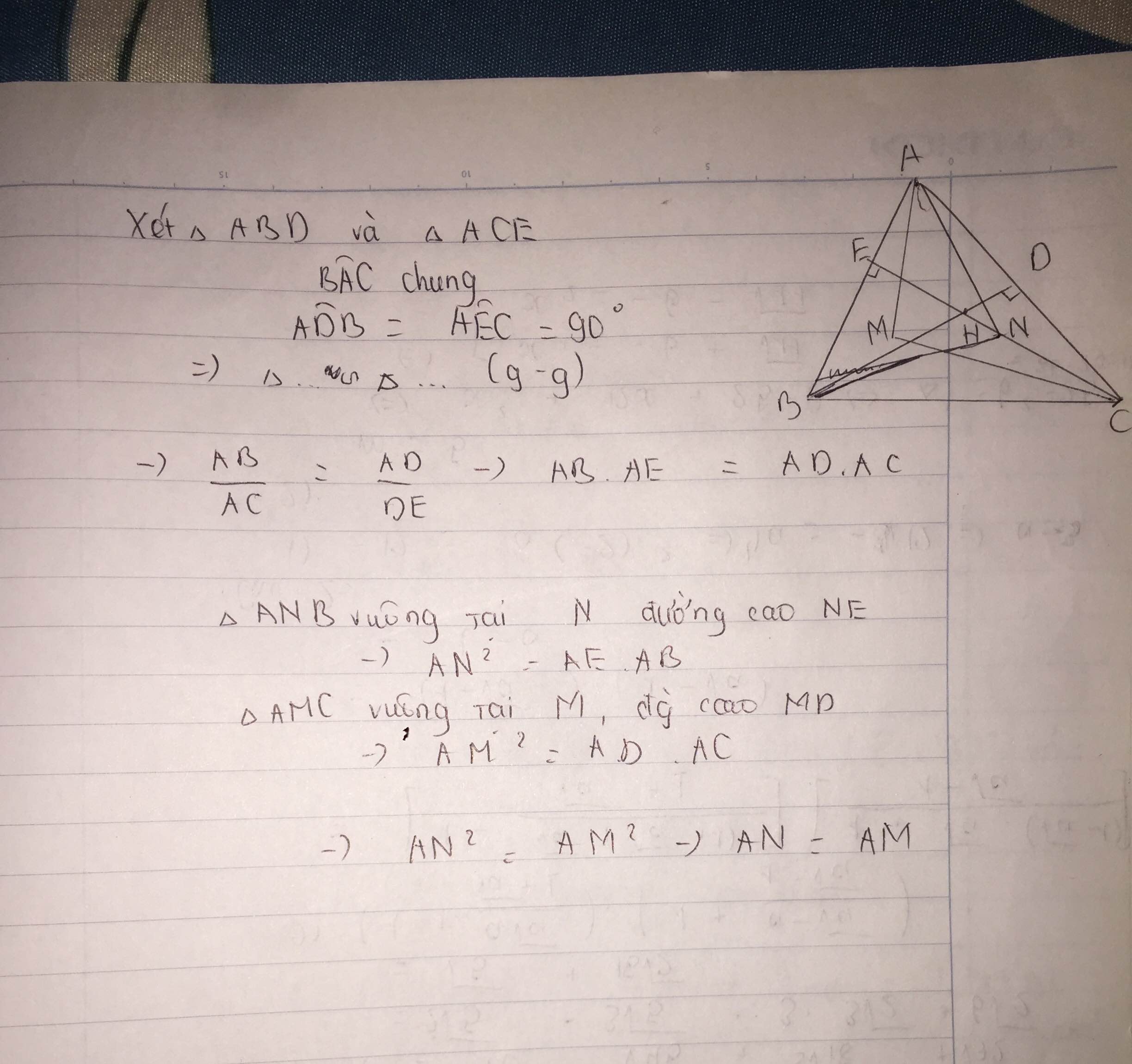Cho tam giác ABC nhọn. Các đường cao AD, BE, CF. Trên BE lấy lần lượt các điểm M, N sao cho góc AMC = góc ANB = 90o. CMR cos2A +cos2B + cos2C <1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
2: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
3: ΔAMC vuông tại M có MD vuông góc AC
nên AD*AC=AM^2
ΔANB vuông tại N có NE vuông góc AB
nên AE*AB=AN^2
=>AM=AN

Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AD\cdot AC=AB\cdot AE\left(1\right)\)
Xét ΔANB vuông tại N có NE là đường cao ứng với cạnh huyền AB
nên \(AB\cdot AE=AN^2\left(2\right)\)
Xét ΔAMC vuông tại M có MD là đường cao ứng với cạnh huyền AC
nên \(AD\cdot AC=AM^2\left(3\right)\)
Từ (1), (2) và (3) suy ra AM=AN

b) ta có: AE/AF = AB/AC ( câu a )
=) AE×AC/AF= AB (1)
Xét tam giác ADB và tam giác CFB có:
Góc ADB= góc CFB
Chung góc ABC
=) Tam giác ADB đồng dạng với tam giác CFB (g-g)
=) BD/AF= AB/AC
(=) BD×BC/BF= AB (2)
Từ (1) và (2) =) cái đề ( đpcm )
hình chữ nhật có diện tích 36 cm2, chiều rộng là 3 cm.Hỏi hình chữ nhât đó có chiều dai gấp mấy lần chiều rộng?

tam giác AMC vuông tại M có MD là đường cao \(\Rightarrow AM^2=AD.AC\left(1\right)\)
tam giác ANB vuông tại N có NE là đường cao \(\Rightarrow AN^2=AE.AB\left(2\right)\)
Xét \(\Delta AEC\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle AEC=\angle ADB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AEC\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AE}{AD}=\dfrac{AC}{AB}\Rightarrow AE.AB=AC.AD\left(3\right)\)
Từ (1),(2),(3) \(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\Rightarrow\Delta AMN\) cân tại A
ủa \(\widehat{AMB}=\widehat{ANC}\) rồi thì △AMN cân rồi cần gì phải đi c/m

Do : Góc ABD = Góc ACE (= 90 - A )
=>  ABD
ABD 
 ACE (2
ACE (2  vuông)
vuông)
=> AD.AC = AE.AB (tỉ lệ đồng dạng)
<=> AM^2 = AN^2 (Hệ thức lượng trong  vuông)
vuông)
<=> AM = AN
Hay  AMN cân tại A.
AMN cân tại A.