Tử của một phân số nhoe hơn mẫu sỗ 5 đon vị. Nếu ta thêm vào tử 17 đơn vị và thêm vào mẫu 2 đơn vị thì được một phân số mới bằng số nghịch đảo của phân số ban đầu. Tìm phân số ban đầu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt tử số của phân số cần tìm là x ta có mẫu của phân số cần tìm là x+5 Ta có phương trình
\(\frac{x+17}{\left(x+5\right)+2}=\frac{x+5}{x}\Leftrightarrow5x=35\Leftrightarrow x=7\)
Vậy tử số của phân số cần tìm là 7
Mẫu của phân số cần tìm là 7+5=12
Phân số cần tìm là \(\frac{7}{12}\)
gọi x (đơn vị) là tử số của phân số ban đầu (x>0)
x+5 (đơn vị) là mẫu số của phân số ban đầu
tử số của phân số lúc sau là x+17(đơn vị)
mẫu số của phân số lúc sau là x+7 (đơn vị)
Ta được phân số mới là số nghịch đảo của phân số ban đầu nên ta có phương trình
x+17/x+7=x+5/x
giải pt ra x = 7

gọi tử số ban đầu là x (x ϵ N*)
mẫu số ban đầu là x+5
tử số sau khi thêm vào 18 đơn vị là x + 18
mẫu số sau khi thêm vào 3 đơn vị là x+5+3 = x+8
vì phân số mới bằng nghịch đảo phân số ban đầu nên ta có phương trình:
\(\dfrac{x+18}{x+8}\) = \(\dfrac{x+5}{x}\)
=> x2 + 18x = x2 + 13x +40
=> 5x - 40 =0
=> x = 8
Vậy phân số ban đầu là \(\dfrac{8}{13}\)

Ta gọi p/s ban đầu là: \(\frac{a}{b}\left(a,b\in Z;b\ne0\right)\)
Theo đề bài ta có: P/s có tử số nhỏ hơn mẫu của nó 5 đơn vị: a+5=b(1)
Nếu ta thêm vào tử 17 đ/v và vào mẫu 2 đơn vị thì đc 1 p/s mới bằng p/s nghịch đảo của p/s ban đầu:\(\frac{a+17}{b+2}=\frac{b}{a}\left(2\right)\)
Từ (1) và (2) ta có hpt: \(\hept{\begin{cases}a+5=b\left(1\right)\\\frac{a+17}{b+2}=\frac{b}{a}\left(2\right)\end{cases}}\)
giải hpt sau ta đc: a=7 và b=12
Vậy p/s ban đầu là: \(\frac{7}{12}\)

Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
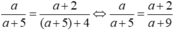
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10

Gọi mẫu số của phân số cần tìm là x ( x khác 0 )
=> Tử số của phân số cần tìm là x - 7
=> Phân số cần tìm có dạng \(\frac{x-7}{x}\)
Thêm cả tử và mẫu 5 đơn vị thì được phân số mới = 1/2
=> Ta có phương trình : \(\frac{x-7+5}{x+5}=\frac{1}{2}\)
<=> \(\frac{x-2}{x+5}=\frac{1}{2}\)
<=> 2( x - 2 ) = x + 5
<=> 2x - 4 = x + 5
<=> 2x - x = 5 + 4
<=> x = 9 ( tmđk )
=> Mẫu số của phân số ban đầu là 9

gọi tử số của phân số cần tìm là a
mẫu số của phân số cần tìm là a+5
nêu thêm tử 17 đơn zị , mẫu 2 đơn zị thì ta có
\(\frac{a+17}{a+7}\)
theo đề bài t có phương trình
\(\frac{a+17}{a+7}=\frac{a+5}{a}\)\(\Leftrightarrow\)\(a\left(a+17\right)=\left(a+5\right)\left(a+7\right)\Leftrightarrow a^2+17a=a^2+7a+5a+35\)
=>\(5a=35=>a=7\)
phâ số cần tìm là \(\frac{7}{12}\)