Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi ps đó là a/b
ta có:a+2/b+2=1/2
->2a+4=b+2
mà a+3=b
->2a+4=a+3+2
->a=1;b=4

Gọi tử số của phân số ban đầu là a, mẫu số của phân số ban đầu là b
Ta có: b=a+5(1)
Ta lại có : (a+3)/(b+3)=2/3 (2)
Thay (1) vào (2) ta được: (a+3)/(a+5+3)=2/3
<=> (a+3)/(a+8)=2/3 <=> 2a+16=3a+9<=> a=7 =>b=a+5=7+5=12
Vậy phân số ban đầu là 7/12
Gọi tử số của phân số ban đầu là a, mẫu số của phân số ban đầu là b
Ta có: b=a+5(1)
Ta lại có : (a+3)/(b+3)=2/3 (2)
Thay (1) vào (2) ta được: (a+3)/(a+5+3)=2/3
<=> (a+3)/(a+8)=2/3 <=> 2a+16=3a+9<=> a=7 =>b=a+5=7+5=12
Vậy phân số ban đầu là 7/12

Ta gọi p/s ban đầu là: \(\frac{a}{b}\left(a,b\in Z;b\ne0\right)\)
Theo đề bài ta có: P/s có tử số nhỏ hơn mẫu của nó 5 đơn vị: a+5=b(1)
Nếu ta thêm vào tử 17 đ/v và vào mẫu 2 đơn vị thì đc 1 p/s mới bằng p/s nghịch đảo của p/s ban đầu:\(\frac{a+17}{b+2}=\frac{b}{a}\left(2\right)\)
Từ (1) và (2) ta có hpt: \(\hept{\begin{cases}a+5=b\left(1\right)\\\frac{a+17}{b+2}=\frac{b}{a}\left(2\right)\end{cases}}\)
giải hpt sau ta đc: a=7 và b=12
Vậy p/s ban đầu là: \(\frac{7}{12}\)

Gọi tử số của phân số ban đầu là a, theo bài ra ta có:
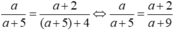
(Điều kiện: a ≠ - 5;a ≠ - 9 )
a(a + 9) = (a + 2)(a + 5)
⇔ a 2 + 9 a = a 2 + 7 a + 10
⇔ 2a = 10 ⇔ a = 5 (Thỏa mãn)
Vậy phân số cần tìm là: 5/10


gọi tử số ban đầu là x (x ϵ N*)
mẫu số ban đầu là x+5
tử số sau khi thêm vào 18 đơn vị là x + 18
mẫu số sau khi thêm vào 3 đơn vị là x+5+3 = x+8
vì phân số mới bằng nghịch đảo phân số ban đầu nên ta có phương trình:
\(\dfrac{x+18}{x+8}\) = \(\dfrac{x+5}{x}\)
=> x2 + 18x = x2 + 13x +40
=> 5x - 40 =0
=> x = 8
Vậy phân số ban đầu là \(\dfrac{8}{13}\)