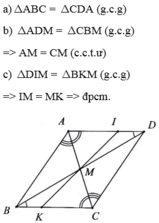
Cho tam giác ABC. Đường thẳng qua A song song với BC cắt đường thẳng qua C song song với AB ở D. Gọi M là giao điểm của AC và BD.
a) Chứng minh: tam giác ABC=tam giác CDA
b) Chứng minh: MA = MC.
c) Trên các đoạn thẳng AD, BC lần lượt lấy các điểm E, N sao cho AE = CN. Chứng minh ME = MN, ba điểm E, M, N thẳng hàng