Bài 17: Cho △ ABC có đường cao AH.Trên AH lấy các điểm K,I sao cho AK=KI=IH .Qua I, K lần lượt vẽ các đường thẳng EF//BC, MN//BC (E, M∈ AB; F, N∈ AC).
a) Tính \(\frac{MN}{BC}\)và \(\frac{EF}{BC}\).
b) Cho biết diện tích tam giác ABC là \(90cm^2\). Tính diện tích tứ giác...
Đọc tiếp
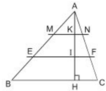
Bài 17: Cho △ ABC có đường cao AH.Trên AH lấy các điểm K,I sao cho AK=KI=IH .Qua I, K lần lượt vẽ các đường thẳng EF//BC, MN//BC (E, M∈ AB; F, N∈ AC).
a) Tính \(\frac{MN}{BC}\)và \(\frac{EF}{BC}\).
b) Cho biết diện tích tam giác ABC là \(90cm^2\). Tính diện tích tứ giác MNFE.
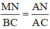
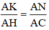
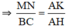
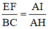
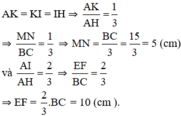
Áp dụng hệ quả Thales với EF//MN//BC có
\(\frac{EF}{BC}=\frac{AF}{AC}=\frac{AK}{AH}=\frac{1}{3}\).Và \(\frac{MN}{BC}=\frac{AN}{AC}=\frac{AI}{AH}=\frac{2}{3}\)
b/ Có \(\frac{S_{AEF}}{S_{ABC}}=\left(\frac{EF}{BC}\right)^2=\frac{1}{9}\Rightarrow S_{AEF}=\frac{1}{9}.90=10cm^2\)
Lại có \(\frac{S_{AMN}}{S_{ABC}}=\left(\frac{MN}{BC}\right)^2=\frac{4}{9}\Rightarrow S_{AMN}=\frac{4}{9}.90=40cm^2\)
Vậy SMNFE=\(S_{ABC}-S_{AEF}-S_{AMN}=90-10-40=40\)cm^2