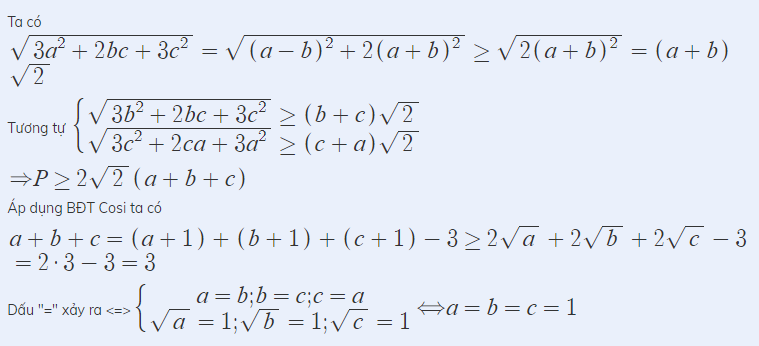Cho a+b+c=3 và a,b>0 Tìm GTLN của \(\sqrt{3a^2+8ab+5b^2}+\sqrt{3b^2+8bc+5c^2}+\sqrt{3c^2+8ca+5a^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PV
19 tháng 2 2018
xin lỗi nha MÌNH sai đề ở chổ \(\sqrt{a}+\sqrt{b}+\sqrt{c}=3\)
GB
1
KN
20 tháng 4 2020
Đặt \(P=\frac{a}{\sqrt{a^2+8bc}}+\frac{b}{\sqrt{b^2+8ca}}+\frac{c}{\sqrt{c^2+abc}}\)
\(=\frac{a^2}{a\sqrt{a^2+8bc}}+\frac{b^2}{b\sqrt{b^2+8ca}}+\frac{c^2}{c\sqrt{c^2+abc}}\)
\(\ge\frac{\left(a+b+c\right)^2}{\left(a\sqrt{a^2+8bc}+b\sqrt{b^2+8ca}+c\sqrt{c^2+8ab}\right)}\)(Theo bất đẳng thức Bunhiacopxki dạng phân thức)
Ta có:
Suy ra 
Ta cần chứng minh \(a^3+b^3+c^3+24abc\le\left(a+b+c\right)^3\)
\(\Leftrightarrow a^2b+b^2c+c^2a+ab^2+bc^2+ca^2\ge6abc\)
Đúng vì \(a^2b+b^2c+c^2a\ge3\sqrt[3]{a^3b^3c^3}=3abc\); \(ab^2+bc^2+ca^2\ge3\sqrt[3]{a^3b^3c^3}=3abc\)
Từ đó suy ra \(\left(a\sqrt{a^2+8bc}+b\sqrt{b^2+8ca}+c\sqrt{c^2+8ab}\right)\le\left(a+b+c\right)^2\)
\(\Rightarrow\frac{\left(a+b+c\right)^2}{\left(a\sqrt{a^2+8bc}+b\sqrt{b^2+8ca}+c\sqrt{c^2+8ab}\right)}\ge1\)
Vậy \(=\frac{a}{\sqrt{a^2+8bc}}+\frac{b}{\sqrt{b^2+8ca}}+\frac{c}{\sqrt{c^2+abc}}\ge1\)
Đẳng thức xảy ra khi a = b = c
TD
1
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2022
\(\left\{{}\begin{matrix}a;b;c\ge0\\a+b+c=1\end{matrix}\right.\) \(\Rightarrow0\le a;b;c\le1\)
\(\Rightarrow a\left(a-1\right)\le0\Rightarrow a^2\le a\)
\(\Rightarrow\sqrt{2a^2+3a+4}=\sqrt{a^2+a^2+3a+4}\le\sqrt{a^2+a+3a+4}=a+2\)
Tương tự và cộng lại:
\(\Rightarrow M\le a+2+b+2+c+2=7\)
\(M_{max}=7\) khi \(\left(a;b;c\right)=\left(0;0;1\right)\) và các hoán vị
D
8 tháng 5 2022
GTNN là tắt của giá trị nhỏ nhất,
Trong bài này bạn biến đổi sao cho biểu thức \(P\ge a\) (số a là số biết trước)
VD: Bạn đưa về dạng nào đó của biểu thức mà nó luôn lớn hơn hoặc bằng \(\dfrac{1}{3}\) Bạn có thể viết \(P\ge\dfrac{1}{3}\) thì GTNN của \(P=\dfrac{1}{3}\) hay \(minP=\dfrac{1}{3}\)
Tìm được GTNN rồi thì bạn tìm ẩn để dấu "=" xảy ra, nghĩa là để BĐT xảy ra dấu =, lúc đó biểu thức P đạt giá trị nhỏ nhất,
VD như: \(minP=\dfrac{1}{3}\) <=> Dấu = xảy ra
<=> x = b (x là ẩn và b là biết trước)
Ở một số bài có thể cho điều kiện của ẩn.
