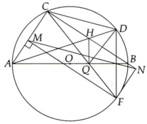
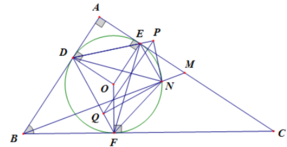
Cho tam giác ABC nội tiếp đường tròn (O), D là 1 điểm trên cạnh BA ( D \(\ne A,B\)). Gọi M,N lần lượt là trung điểm các cạnh CB,AC. Đường thẳng MN cắt (O) tại các điểm P,Q (P,Q lần lượt thuộc cung CB và cung AC). Đường tròn ngoại tiếp tam giác BDP cắt CB tại I (khác B). Các đường thẳng DI và AC cắt nhau tại K.
a) C/m: Tứ giác CIPK nội tiếp
b) CMR: PK.QC =QB.PD .
c) Đường thẳng AP cắt đường tròn ngoại tiếp tam giác BDP tại G (khác P). Đường thẳng IG cắt đường thẳng BA tại E. Cmr khi D di chuyển trên BA thì \(\frac{AD}{AE}\) không đổi.