Giải giúp mk bài này dzới mọi ngừi 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
14 tháng 10 2021
a, Giả sử: Cz // Ax // By
Do Cz // Ax \(\Rightarrow\widehat{A}+\widehat{C_1}=180^o\)(2 góc TCP)
\(\Rightarrow80^o+\widehat{C_1}=180^o\)
\(\Rightarrow\widehat{C_1}=180^o-80^o=100^o\)
Do Cz // By \(\Rightarrow\widehat{C_2}=\widehat{B}=35^o\)(2 góc so le trong)
Ta thấy: \(\widehat{ACB}=\widehat{C_1}+\widehat{C_2}=100^o+35^o=135^o\)
b, Do d // AC \(\Rightarrow\widehat{ACB}+\widehat{EBC}=180^o\)(2 góc TCP)
\(\Rightarrow135^o+\widehat{EBC}=180^o\)
\(\Rightarrow\widehat{EBC}=180^o-135^o=45^o\)
7 tháng 10 2021
Vì a//b( gt)
Mà c vuông góc với a(gt)
=> c vuông góc với b( từ vuông góc đến //)
=> Góc ABC = 90°
Vì a//b (gt)
=>góc dDA = góc BCD(đồng vị)
Mà góc dDA =55° (gt)
=> góc BCD =55°
Vì a//b(gt)
=> góc BCD + góc CDA =180°( trong cùng phía)
Mà góc BCD = 55°(cmt)
=> góc CDA = 180°- 55°=125°
7 tháng 10 2021
a // b và a\(\perp\) c
\(\Rightarrow b\perp c\)
\(\Rightarrow\widehat{ABC}=90^o\)
a // b
\(\Rightarrow\widehat{BCD}=\widehat{dDA}=55^o\) ( đồng vị )
\(\widehat{CDA}=125^o\) ( kề bù góc dDA )
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}=\sqrt{2^2.5}-\sqrt{3^2.5}+\sqrt{\left(\sqrt{5}+1\right)^2}=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1=1\)
\(\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}=2\sqrt{5}-2-\left|\sqrt{5}-2\right|=2\sqrt{5}-2-\sqrt{5}+2=\sqrt{5}\)
\(\left(\sqrt{27}+3\sqrt{12}-2\sqrt{3}\right):\sqrt{3}=\left(3\sqrt{3}+6\sqrt{3}-2\sqrt{3}\right):\sqrt{3}=7\sqrt{3}:\sqrt{3}=7\)
\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{5^2.2}-3\sqrt{2^2.2}+\sqrt{\left(\sqrt{2}+1\right)^2}=5\sqrt{2}-6\sqrt{2}+\sqrt{2}+1=1\)
2 tháng 8 2021
1) \(A=\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}\)
\(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1\)
=1
2) Ta có: \(B=\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=2\sqrt{5}-2-\sqrt{5}+2\)
\(=\sqrt{5}\)
15 tháng 6 2021
a) \(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\)=4 - \(\dfrac{x}{3}\)
<=>\(\dfrac{2x}{3}\)+\(\dfrac{2x-1}{6}\) - 4+\(\dfrac{x}{3}\)=0
<=>\(\dfrac{2x.2+2x-1-4.6+x.2}{6}\)=0
=>4x-2x-24+2x=0
<=>4x-24=0
<=>4x=24
<=>x=6
Vậy x=6
15 tháng 6 2021
b)\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)=1 - \(\dfrac{2\left(x-1\right)}{3}\)
<=>\(\dfrac{x-1}{2}\)+\(\dfrac{x-1}{4}\)-1+\(\dfrac{2\left(x-1\right)}{3}\)=0
<=>\(\dfrac{6.\left(x-1\right)+3\left(x-1\right)-1.12+4.2\left(x-1\right)}{12}\)=0
=>6x-6+3x-3-12+4x-4+2x-2=0
<=>15x-27=0
<=>15x=27
<=>x=\(\dfrac{9}{5}\)
Vậy x=\(\dfrac{9}{5}\)
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải.
c.
$x^3-3x^2+3x-1=0$
$\Leftrightarrow (x-1)^3=0$
$\Leftrightarrow x-1=0$
$\Leftrightarrow x=1$
Vậy pt có tập nghiệm $S=\left\{1\right\}$
d. ĐKXĐ: $x\neq \frac{-1}{3}; -3$
PT $\Leftrightarrow \frac{(3x-1)(x+3)+(x-3)(3x+1)}{(3x+1)(x+3)}=2$
$\Leftrightarrow \frac{6x^2-6}{3x^2+10x+3}=2$
$\Leftrightarrow 6x^2-6=2(3x^2+10x+3)$
$\Leftrightarrow 20x+12=0$
$\Leftrightarrow x=\frac{-3}{5}$ (tm)
Vậy tập nghiệm của pt là $S=\left\{\frac{-3}{5}\right\}$
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Bài 2:
a.
\(\left\{\begin{matrix} 2x-3y=11\\ 5x-4y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 10x-15y=55\\ 10x-8y=6\end{matrix}\right.\)
\(\Rightarrow (10x-8y)-(10x-15y)=6-55\)
\(\Leftrightarrow 7y=-49\Leftrightarrow y=-7\)
\(x=\frac{3y+11}{2}=\frac{3.(-7)+11}{2}=-5\)
Vậy hpt có nghiệm $(x,y)=(-5,-7)$
b. Không đủ cơ sở để tìm $x,y$
c.
\(\left\{\begin{matrix} 5x+3y=\lambda\\ -x+\lambda y=-8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x+3y=\lambda\\ -5x+5\lambda y=-40\end{matrix}\right.\)
\(\Rightarrow (3+5\lambda)y=\lambda-40\)
Nếu $\lambda = \frac{-3}{5}$ thì $0.y=\frac{-203}{5}$ (vô lý) nên hpt vô nghiệm
Nếu $\lambda \neq \frac{-3}{5}$ thì:
$y=\frac{\lambda - 40}{3+5\lambda}$
$x=8+\lambda y=\frac{\lambda ^2+24}{5\lambda +3}$
đây nha
27 tháng 11 2021
1. Bài giải:
Đổi 14m4cm = 1404cm
Mỗi cạnh của hình vuông là:
1404 : 4 = 351 ( cm )
Diện tích hình vuông là:
351 x 351 = 123201 ( cm2 )
Đáp số: 123201 cm2
Note: cm2 = cm vuông
TL
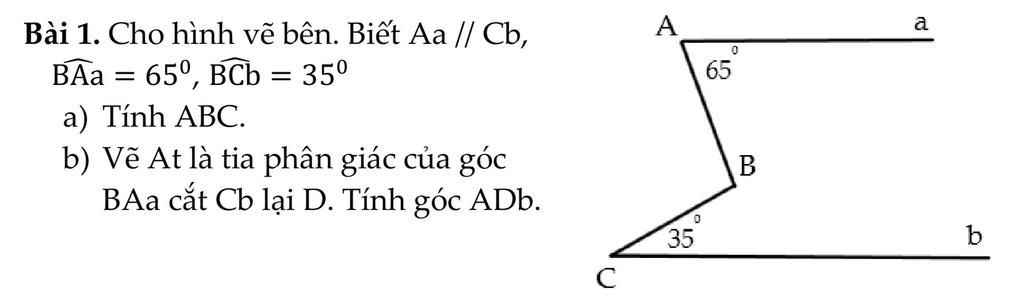
a, Kẻ Bx//Aa//Cb
\(\Rightarrow\widehat{ABx}=\widehat{BAa}=65^0;\widehat{CBx}=\widehat{BCb}=35^0\left(so.le.trong\right)\\ \Rightarrow\widehat{ABC}=\widehat{ABx}+\widehat{CBx}=65^0+35^0=100^0\)
b, Vì At là p/g góc BAa nên \(\widehat{DAa}=\dfrac{1}{2}\widehat{BAa}=32,5^0\)
Vì Aa//Cb nên \(\widehat{DAa}+\widehat{ADb}=180^0\left(trong.cùng.phía\right)\)
\(\Rightarrow\widehat{ADb}=180^0-32,5^0=147,5^0\)
Có đúng ko CTV??