K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 10 2021
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{b}-1=\dfrac{c}{d}-1\Rightarrow\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
\(\Rightarrow\dfrac{b}{a-b}=\dfrac{d}{c-d}\Rightarrow\dfrac{2b}{a-b}=\dfrac{2d}{c-d}\)
\(\Rightarrow\dfrac{2b}{a-b}+1=\dfrac{2d}{c-d}+1\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\) (đpcm)
18 tháng 10 2021
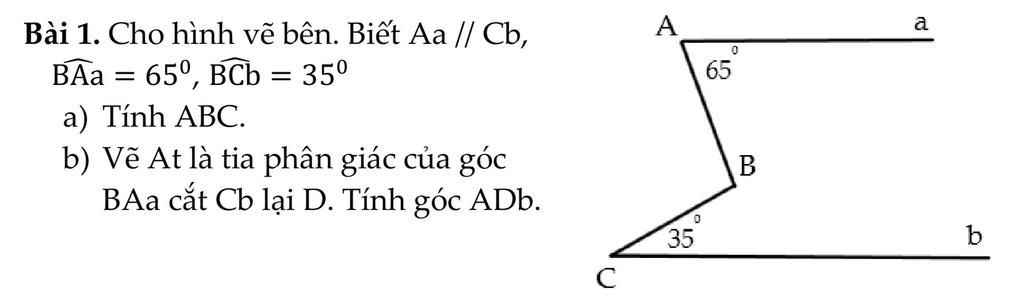
a, Kẻ Bx//Aa//Cb
\(\Rightarrow\widehat{ABx}=\widehat{BAa}=65^0;\widehat{CBx}=\widehat{BCb}=35^0\left(so.le.trong\right)\\ \Rightarrow\widehat{ABC}=\widehat{ABx}+\widehat{CBx}=65^0+35^0=100^0\)
b, Vì At là p/g góc BAa nên \(\widehat{DAa}=\dfrac{1}{2}\widehat{BAa}=32,5^0\)
Vì Aa//Cb nên \(\widehat{DAa}+\widehat{ADb}=180^0\left(trong.cùng.phía\right)\)
\(\Rightarrow\widehat{ADb}=180^0-32,5^0=147,5^0\)
LN
14 tháng 10 2021
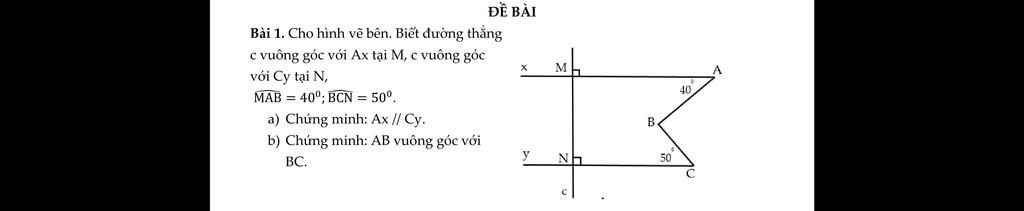
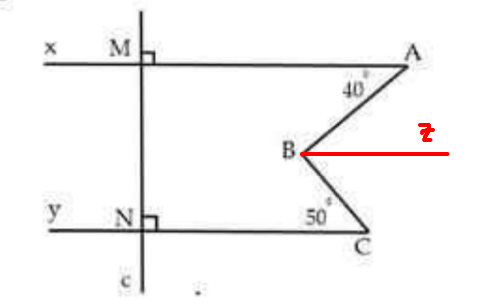
a, Do MN ⊥ Ax , MN ⊥ Cy => Ax // Cy ( từ vuông góc đến song song)
b, Kẻ Bz // AB // Cy
Do Ax // Bz \(\Rightarrow\widehat{A}=\widehat{B_1}=40^o\)(2 góc so le trong)
Do Bz // Cy \(\Rightarrow\widehat{B_2}=\widehat{C}=50^o\)
Ta thấy: \(\widehat{ABC}=\widehat{B_1}+\widehat{B_2}=40^o+50^o=90^ohayAB\perp BC\left(dpcm\right)\)
GW
13 tháng 10 2021
Từ \(\frac{x}{2}=\frac{y}{3}=\frac{x}{2}.\frac{1}{2}=\frac{y}{3}.\frac{1}{2}\)\(\Rightarrow\)\(\frac{x}{4}=\frac{y}{6}\)( 1 )
Từ \(\frac{y}{2}=\frac{z}{5}=\frac{y}{2}.\frac{1}{3}=\frac{z}{5}.\frac{1}{3}\)\(\Rightarrow\)\(\frac{y}{6}=\frac{z}{15}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra : \(\frac{x}{4}=\frac{y}{6}=\frac{z}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{4}=\frac{y}{6}=\frac{z}{15}=\frac{x}{4}=\frac{3y}{18}=\frac{5z}{75}=\frac{x+3y-5z}{4+18-75}=\frac{-106}{-53}=2\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{4}=2\\\frac{y}{6}=2\\\frac{z}{15}=2\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=8\\y=12\\z=30\end{cases}}\)
13 tháng 10 2021
\(\frac{x}{2}\)=\(\frac{y}{3}\)⇒\(\frac{x}{4}\)=\(\frac{y}{6}\)
\(\frac{y}{2}\)=\(\frac{z}{5}\)⇒\(\frac{y}{6}\)=\(\frac{z}{15}\)
⇒\(\frac{x}{4}\)=\(\frac{y}{6}\)=\(\frac{z}{15}\)=\(\frac{x+3y-5z}{4+18-75}\)=\(\frac{106}{-53}\)=2
⇒x=8,y=12,z=30
Nhớ chọn mình nha
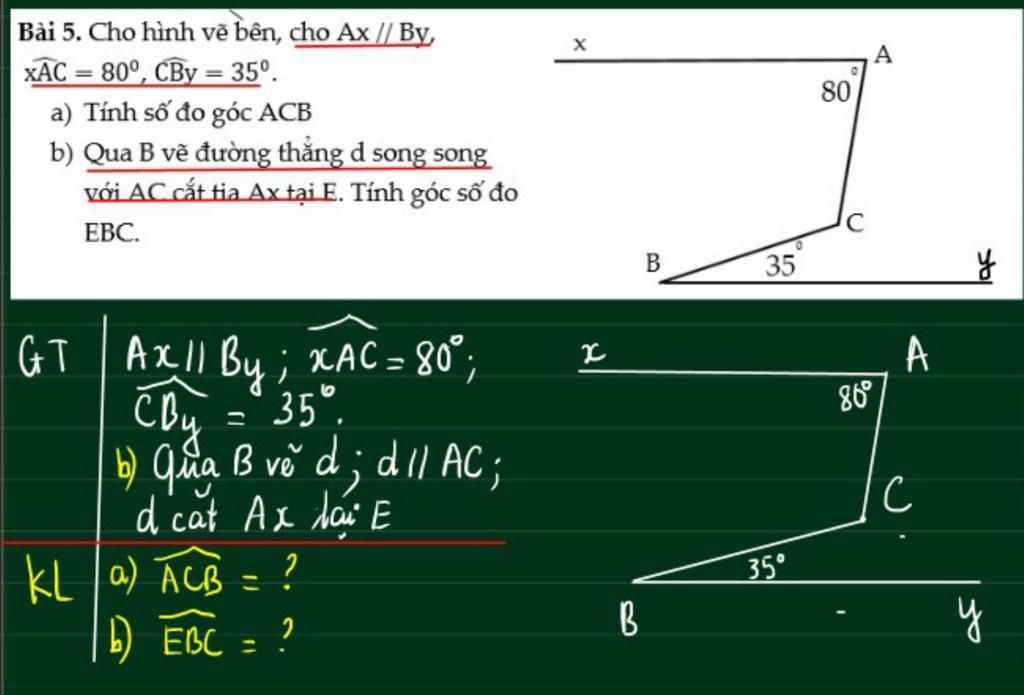
a, Giả sử: Cz // Ax // By
Do Cz // Ax \(\Rightarrow\widehat{A}+\widehat{C_1}=180^o\)(2 góc TCP)
\(\Rightarrow80^o+\widehat{C_1}=180^o\)
\(\Rightarrow\widehat{C_1}=180^o-80^o=100^o\)
Do Cz // By \(\Rightarrow\widehat{C_2}=\widehat{B}=35^o\)(2 góc so le trong)
Ta thấy: \(\widehat{ACB}=\widehat{C_1}+\widehat{C_2}=100^o+35^o=135^o\)
b, Do d // AC \(\Rightarrow\widehat{ACB}+\widehat{EBC}=180^o\)(2 góc TCP)
\(\Rightarrow135^o+\widehat{EBC}=180^o\)
\(\Rightarrow\widehat{EBC}=180^o-135^o=45^o\)