Cho \(\Delta ABC\). Vẽ ở ngoài tam giác các hình vuông ABDE, ACFH.
a) CM: EC=BH
b)\(EC\perp BH\)
c) Gọi M,N là tâm các hình vuông ABDE, ACFH. Gọi I là trung điểm BC. Tam giác MNI là tam giác gì, vì sao?
Các bạn giúp mình nhe! Cảm ơn nhiều ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 1 2017
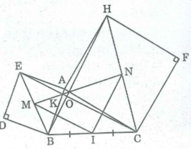
* Trong ∆ EBC , ta có: M là trung điểm EB (tính chất hình vuông)
I trung điểm BC (gt)
Nên MI là đường trung bình của ΔEBC
⇒ MI = 1/2 EC và MI // EC (tính chất đường trung bình của tam giác).
Trong ∆ BCH, ta có: I trung điểm BC (gt)
N trung điểm của CH (tính chất hình vuông)
Nên NI là đường trung bình của ∆ BCH
⇒ NI = 1/2 BH và NI // BH (tính chất đường trung bình của tam giác)
Mà BH = CE (chứng minh trên)
Suy ra: MI = NI nên ∆ INM cân tại I
MI // EC (chứng minh trên)
EC ⊥ BH (chứng minh trên)
Suy ra: MI ⊥ BH. Mà NI // BH (chứng minh trên)
Suy ra: MI ⊥ NI hay ∠ (MIN) = 90 0
Vậy ∆ MIN vuông cân tại I.
CH
Cô Hoàng Huyền
Admin
VIP
21 tháng 11 2016
a. Ta thấy \(\widehat{EAC}=\widehat{BAH}\left(=\widehat{BAC}+90^o\right)\)
Vậy nên \(\Delta EAC=\Delta BAH\left(c-g-c\right)\)
Từ đó suy ra \(\widehat{ACE}=\widehat{AHB}\)
Vì \(\widehat{AHB}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{ACE}+\widehat{JHF}+\widehat{F}+\widehat{FCA}=270^o\Rightarrow\widehat{HJC}=90^o\)
Vậy \(EC\perp BH.\)
b. Ta thấy \(O_1\) là trung điểm EB. Vậy thì O1I là đường trung bình của tam giác BEC hay O1I // EC. Tương tự O2I // BH.
Lại có \(EC\perp BH\) nên \(O_1I\perp O_2I.\)
Vậy tam giác O1O2I là tam giác vuông tại I.
a. Ta có: ˆBAH=ˆBAC+ˆCAH=ˆBAC+900
ˆEAC=ˆBAC+ˆBAE=ˆBAC+900
Suy ra: ˆBAH=ˆEAC
– Xét ∆ BAH và ∆ EAC:
BA = EA (vì ABDE là hình vuông)
ˆBAH=ˆEAC (chứng minh trên)
AH = AC (vì ACFH là hình vuông)
Do đó: ∆ BAH = ∆ EAC (c.g.c)
⇒ BH = EC
Gọi giao điểm của EC với AB và BH lần lượt là K và O.
ˆAEC=ˆABH (vì ∆ BAH = ∆ EAC) (1)
hay ˆAEK=ˆOBK
– Trong ∆ AEK ta có: ˆEAK=900
⇒ˆAEK+ˆAKE=900
Um... phần a và b mình làm rồi nhưng còn phần c chưa giải được ._.