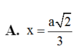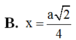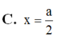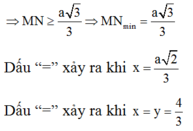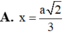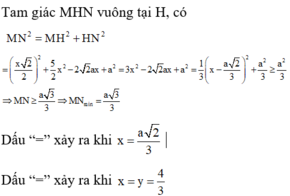lấy M thuộc p1 :y=x^2-4x+3 và N thuộc p2: y= (x-5)^2 sao cho đoạn MN ngắn nhất.tính MN ???? Help meeeeeeeeeee
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 7 2020
Phương trình tham số d1: \(\left\{{}\begin{matrix}x=1+2t\\y=3+3t\\z=2t\end{matrix}\right.\)
Phương trình tham số d2: \(\left\{{}\begin{matrix}x=5+6t'\\y=4t'\\z=5-5t'\end{matrix}\right.\)
Gọi (Q) là mặt phẳng song song (P) và cách (P) 1 khoảng bằng 2 \(\Rightarrow\) pt có dạng \(x-2y-2z-d=0\) (\(d\ne1\))
Gọi \(A\left(d;0;0\right)\) là 1 điểm thuộc (Q)
\(d\left(A;\left(P\right)\right)=2\Leftrightarrow\frac{\left|d+1\right|}{\sqrt{1+4+4}}=2\Leftrightarrow\left|d+1\right|=6\Rightarrow\left[{}\begin{matrix}d=5\\d=-7\end{matrix}\right.\)
Có 2 mp (Q) thỏa mãn: \(\left[{}\begin{matrix}x-2y-2z-5=0\\x-2y-2z+7=0\end{matrix}\right.\)
M là giao điểm (Q) và d1 nên tọa độ M là ...
N là giao điểm (Q) và d2 nên tọa độ N là ...
CM
4 tháng 8 2018
Đáp án A
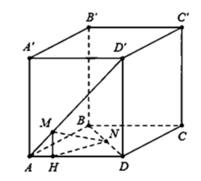
Kẻ:
M H ⊥ A D ⇒ M H = A H = x 2 2 ⇒ H D = a − x 2 2
Tam giác HND có
H N 2 = D N 2 − 2 D N . H D . c o s 2 N D H ^
= a − x 2 2 2 + x 2 − 2 x a − x 2 2 = 5 2 x 2 − 2 2 a x + a 2
Vì:
M H ⊥ A D ⇒ M H / / A A ' ⇒ M H ⊥ A B C D ⇒ M H ⊥ H N
Tam giác MHN vuông tại H, có M N 2 = M H 2 + H N 2
= x 2 2 2 + 5 2 x 2 − 2 2 a x + a 2 = 3 x 2 − 2 2 a x + a 2 = 1 3 x − a 2 3 2 + a 2 3 ≥ a 2 3 ⇒ M N ≥ a 3 3 ⇒ M N min = a 3 3
Dấu “=” xảy ra khi
x
=
a
2
3
MH
14 tháng 9 2021
c)\(\left(xy^2-1\right)\left(x^2y+5\right)\)
\(=x^3y^3+5xy^2-x^2y-5\)
d)\(4\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)\left(4x^2+1\right)\)
\(=4\left(x^2-\dfrac{1}{4}\right)\left(4x^2+1\right)\)
\(=4\left(4x^4+x^2-x-\dfrac{1}{4}\right)\)
\(=16x^4+4x^2-4x-1\)
