Giúp mình với, mình cần gấp :)))
cho tam giác ABC vuông tại A có AB + BC = AC.căn 3. Tính số đo góc B và C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2023
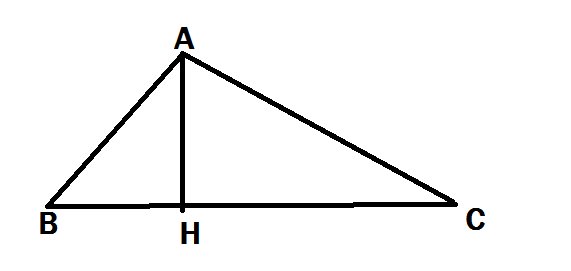
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{9}=\dfrac{1}{AB^2}+\dfrac{1}{25}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{16}{225}\)
\(\Leftrightarrow AB=\dfrac{15}{4}\)
- \(AH.BC=AB.AC\)
\(3.BC=\dfrac{15}{4}.5\)
\(BC=6,25\)
- \(CH=\dfrac{AC^2}{BC}=4\)
=> BH = 6,25 - 4 = 2,25
Ta có:
\(AB+BC=AC\sqrt{3}\)
=> \(\frac{AC}{BC}\sqrt{3}-\frac{AB}{BC}=1\)
=> \(\sqrt{3}\cos\widehat{C}-\sin\widehat{C}=1\)
=> \(\sqrt{3}\cos\widehat{C}-1=\sin\widehat{C}\)
Mặt khác: \(\sin^2\widehat{C}+\cos^2\widehat{C}=1\)
<=> \(\left(\sqrt{3}\cos\widehat{C}-1\right)^2+\cos^2\widehat{C}=1\)
<=> \(4\cos^2\widehat{C}-2\sqrt{3}\cos\widehat{C}=0\)( \(0^o< \widehat{C}< 90^o\))
<=> \(2\cos\widehat{C}-\sqrt{3}=0\)
<=> \(\cos\widehat{C}=\frac{\sqrt{3}}{2}\)
<=> \(\widehat{C}=30^o\)=> \(\widehat{B}=60^o\)
em cảm ơn cô nhiều lắm ạ <3