Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét tứ giác AEMF có
\(\widehat{EAF}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{AFM}=90^0\)(gt)
Do đó: AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Xét ΔABC có
M là trung điểm của BC(gt)
MF//AB(cùng vuông góc với AC)
Do đó: F là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
F là trung điểm của AC(cmt)
Do đó: MF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: \(MF=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà AE=MF(AFME là hình chữ nhật)
nên \(AE=\dfrac{AB}{2}\)
mà A,E,B thẳng hàng(gt)
nên E là trung điểm của AB
Ta có: F là trung điểm của NM(gt)
nên \(MN=2\cdot MF\)(1)
Ta có: E là trung điểm của AB(cmt)
nên AB=2AE(2)
Ta có: AEMF là hình chữ nhật(cmt)
nên MF=AE(Hai cạnh đối)(3)
Từ (1), (2) và (3) suy ra MN=AB
Xét tứ giác ABMN có
MN//AB(cùng vuông góc với AC)
MN=AB(cmt)
Do đó: ABMN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
a, xét tứ giác BEMF có : góc CEF = góc MEB = góc MFB = 90
=> BEMF là hình chữ nhật (dh)
b, MF _|_ BA
BC _|_ AB
=> MF // BC
M là trung điểm của AC (gt)
=> MF là đường trung bình của tam giác ABC (đl)
=> F là trung điểm của AB
F Là trung điểm của MN
=> BMAN là hình bình hành (dh)
MN _|_ AB
=> BMAN là hình thoi (dh)
c,
S BEMF = 6X10= 60
ht
a) Xét tứ giác ADME có :
Góc A = 900 ( tam giác ABC vuông tại A )
Góc D = 900 ( MD vuông góc AB )
Góc E = 900 ( ME vuông góc AC )
Do đó tứ giác ADME là hình chữ nhật
b) Chứng minh đúng D, E là trung điểm của AB ; AC
Chứng minh đúng DE là đường trung bình của tam giác
ABC nên DE song song và \(DE=\frac{BC}{2}\)
Cho nên DE song song với BM và DE = BM
=> Tứ giác BDME là hình bình hành
c) Xét tứ giác AMCF có :
E là trung điểm MF ( vì M đối xứng với F qua E )
Mà E là trung điểm của AC ( cmt )
Nên tứ giác AMCF là hình bình hành
Ta có AC vuông góc MF ( vì ME vuông góc AC )
Do đó tứ giác AMCF là hình thoi
d) Chứng minh đúng tứ giác ABNE là hình chữ nhật
Gọi O là giao điểm hai đường chéo AN và BE của hình chữ nhật ABNE
trong tam giác vuông BKE có KO là trung tuyến ứng với cạnh huyền BE
nên \(KO=\frac{BE}{2}\)
mà BE = AN ( đường chéo hình chữ nhật ) nên \(KO=\frac{AN}{2}\)
trong tam giác AKN có trung tuyến KO bằng nửa cạnh AN
nên tam giác AKN vuông tại A
Vậy AK vuông góc KN
Xét tứ giác AFME có
\(\widehat{EAF}=90^0\)
\(\widehat{AEM}=90^0\)
\(\widehat{AFM}=90^0\)
Do đó: AFME là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
a: Xét tứ giác ANKM có
\(\widehat{ANK}=\widehat{AMK}=\widehat{MAN}=90^0\)
Do đó: ANKM là hình chữ nhật
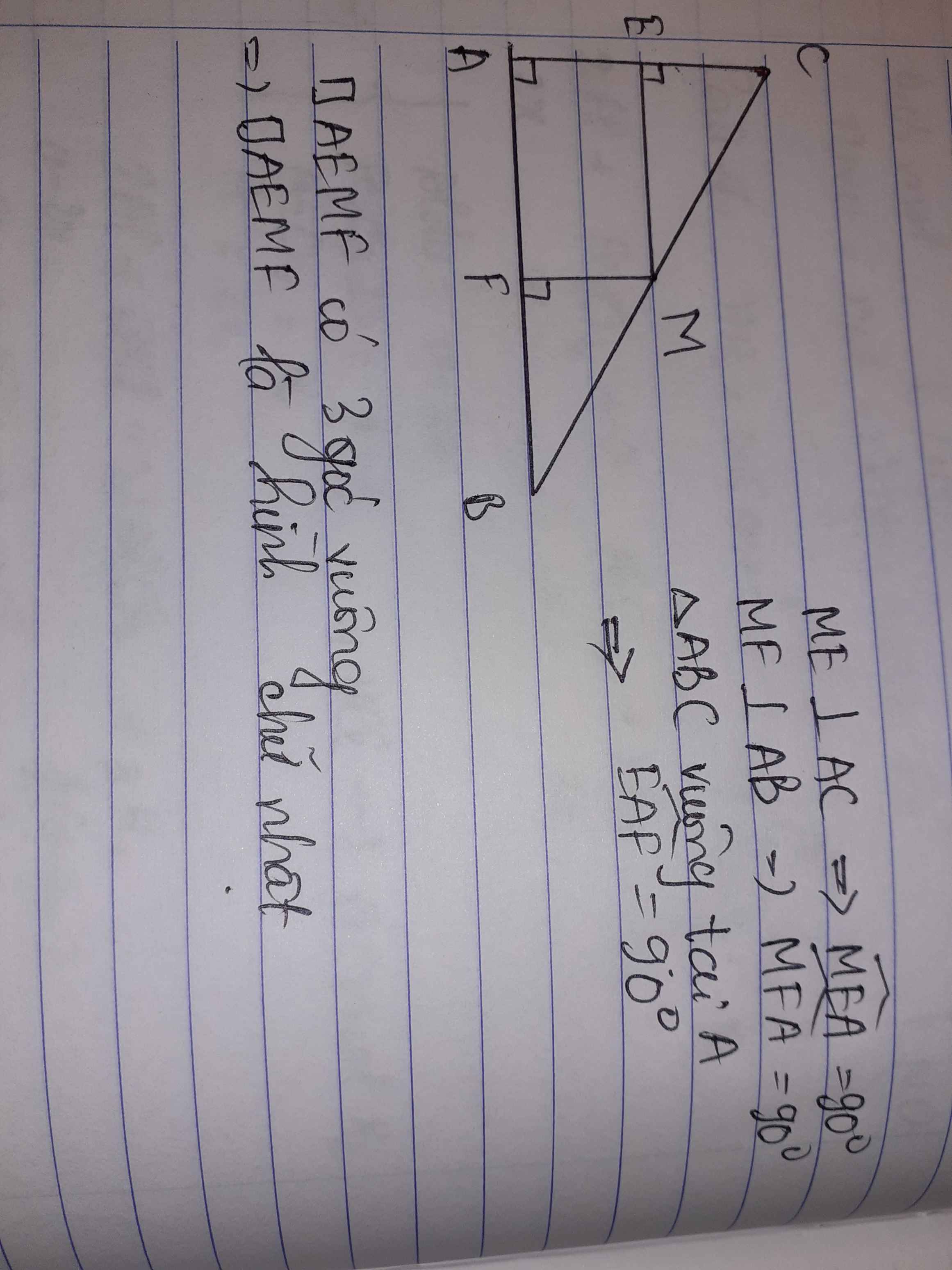
a, tam giác ABC vuông tại C (gt)
=> góc ACB = 90 (đn)
có ME _|_ AC (gt) => góc MEC = 90 (đn)
MF _|_ BC (gt) => góc MFC = 90 (đn)
xét tứ giác EMFC
=> EMFC là hình chữ nhật (dấu hiệu)
=> CM = EF (tính chất)
b, M là trung điểm của AB (Gt)
=> CM là trung tuyến (đn/)
tam giác ABC vuông tại C (Gt)
=> CM = AM = AB/2 (đl)
xét tam giác AME và tam giác CME có : EM chung
góc MEA = góc MEC = 90
=> tam giác AME = tam giác CME (ch-cgv)
=> AE = EC (đn)
E thuộc AC
=> E là trung điểm của AC (đn)
c, có ME _|_ AC
=> MD _|_ AC ; xét tứ giác ADCM
=> ADCM là hình thoi (dấu hiệu)
h