cho ΔABC có góc B =60o , AB=6cm,AC=4cm . tính AC (ΔABC không vuông)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TQ
2
1 tháng 11 2019
Kẻ đường cao AH
Ta thấy :
\(\frac{BH}{AB}=cosB\Rightarrow BH=ABcosB=6cos60^o=3\left(cm\right)\)
\(\frac{AH}{AB}=sinB\Rightarrow AH=ABsinB=6sin60^o=3\sqrt{3}\left(cm\right)\)
\(CH=BC-BH=4-3=1\left(cm\right)\)
Áp dụng định lí Pitago cho tam giác vuông AHC
\(AC=\sqrt{AH^2+CH^2}=\sqrt{\left(3\sqrt{3}^2\right)+1^2}=2\sqrt{7}\left(cm\right)\)
Chúc bạn học tốt !!!
I
2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 7 2021
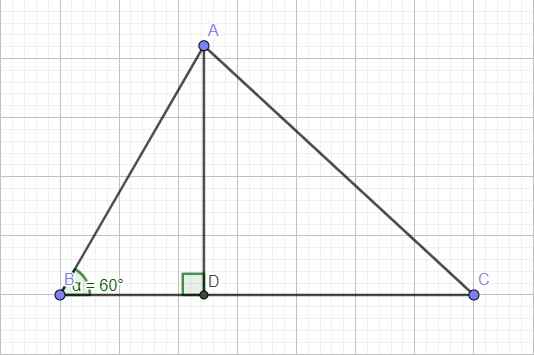
Kẻ đường cao AD, đặt \(AB=x>0\) ; \(BD=y>0\)
\(\Rightarrow AC=12-x\) ; \(CD=8-y\)
Trong tam giác vuông ABD:
\(BD=AB.cosB\Leftrightarrow y=x.cos60^0=\dfrac{x}{2}\) \(\Rightarrow CD=8-\dfrac{x}{2}\)
Theo định lý Pitago:
\(\left\{{}\begin{matrix}AD^2=AB^2-BD^2\\AD^2=AC^2-CD^2\end{matrix}\right.\) \(\Rightarrow AB^2-BD^2=AC^2-CD^2\)
\(\Leftrightarrow x^2-\left(\dfrac{x}{2}\right)^2=\left(12-x\right)^2-\left(8-\dfrac{x}{2}\right)^2\)
\(\Leftrightarrow16x-80=0\)
\(\Rightarrow x=5\)
Vậy \(\left\{{}\begin{matrix}AB=5\\AC=7\end{matrix}\right.\)
6 tháng 2 2023
a: AC-BC<AB<AC+BC
=>5<AB<8
mà AB>6
nên AB=7cm
b: AB-AC<BC<AB+AC
=>2<BC<14
mà BC<4
nên BC=3cm
1 tháng 7 2023
a: Xét ΔCMD vuông tại M và ΔCAB vuông tại A có
góc C chung
=>ΔCMD đồng dạng với ΔCAB
b: Xét ΔBMI vuông tại M và ΔBAC vuông tại A có
góc MBI chung
=>ΔBMI đồng dạng với ΔBAC
=>BM/BA=BI/BC
=>BM*BC=BA*BI
c: ΔCMD đồng dạng với ΔCAB
=>CM/CA=CD/CB
=>CM/CD=CA/CB
=>ΔCMA đồng dạng với ΔCDB
=>S CMA/S CDB=(CA/CB)^2=1/4
=>S CMA=15cm2
NN
1
22 tháng 12 2021
Vì \(\Delta ABC\) vuông tại \(A\)
\(\Rightarrow\) \(AB , AC\) là hai cạnh góc vuông còn \(BC\) là cạnh huyền
Áp dụng định lý Py \(-\) ta \(-\) go vào \(\Delta ABC\) , ta có :
\(BC^2=AB^2+AC^2=3^2+4^2=9+16=25=5^2\)
\(\Rightarrow\) \(BC=5\)
Vậy \(BC = 5 cm\)
9 tháng 6 2021
a, \(\Delta ABC\sim\Delta CBD\)
\(\dfrac{AB}{CB}=\dfrac{BC}{BD}=\dfrac{4}{6}=\dfrac{6}{4+5}=\dfrac{2}{3}\)
b, \(\dfrac{AC}{CD}=\dfrac{AB}{CB}=\dfrac{2}{3}\)
\(\Rightarrow CD=\dfrac{3AC}{2}=\dfrac{15}{2}\)
-Chúc bạn học tốt-
Lời giải:
Kẻ đường cao $AH$
Ta thấy:
$\frac{BH}{AB}=\cos B\Rightarrow BH=AB\cos B=6\cos 60^0=3$ (cm)
$\frac{AH}{AB}=\sin B\Rightarrow AH=AB\sin B=6\sin 60^0=3\sqrt{3}$ (cm)
$CH=BC-BH=4-3=1$ (cm)
Áp dụng định lý Pitago cho tam giác vuông $AHC$:
$AC=\sqrt{AH^2+CH^2}=\sqrt{(3\sqrt{3})^2+1^2}=2\sqrt{7}$ (cm)
Hình vẽ: