1. Trong mặt phẳng Oxy cho hình bình hành ABCD , tâm O là gốc tọa độ , đỉnh A(3;1) , đỉnh B(1;2)
a. Xác định tọa độ 2 đỉnh C và D
b. Viết phương trình đường thẳng chứa các cạnh của hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DB}=\overrightarrow{AC}-\overrightarrow{AB}-\overrightarrow{BD}\)
\(\Rightarrow2\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{BD}\Rightarrow\overrightarrow{AB}=\frac{1}{2}\left(\overrightarrow{AC}-\overrightarrow{BD}\right)=\left(5;-\frac{7}{2}\right)\)

Áp dụng quy tắc hình bình hành ta có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AD}=\widehat{AC}\\\overrightarrow{AD}-\overrightarrow{AB}=\overrightarrow{BD}\end{matrix}\right.\)
Từ hệ trên suy ra:
\(\overrightarrow{2AB}=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)-\left(\overrightarrow{AD}-\overrightarrow{AB}\right)=\overrightarrow{AC}-\overrightarrow{BD}\)
\(\Leftrightarrow\overrightarrow{AB}=\frac{1}{2}\left(\overrightarrow{AC}-\overrightarrow{BD}\right)=\frac{1}{2}\left[7-\left(-3\right);-3-4\right]=\left(5;\frac{-7}{2}\right)\)

Đáp án B
Gọi hình bình hành là ABCD và
d:x+ y-1 = 0, ∆: 3x – y+ 5= 0 .
Không làm mất tính tổng quát giả sử
![]()
Ta có : ![]() . Vì I(3;3) là tâm hình bình hành nên C(7;4) ;
. Vì I(3;3) là tâm hình bình hành nên C(7;4) ; ![]()
=> Đường thẳng ACcó pt là: x- 4y + 9= 0.
Do ![]() => Đường thẳng BC đi qua điểm C và có vtpt
=> Đường thẳng BC đi qua điểm C và có vtpt ![]() có pt là: 3x – y- 17= 0.
có pt là: 3x – y- 17= 0.
Khi đó :
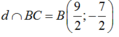
Ta có:
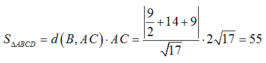

Đáp án B
![]() => Đường thẳng AB có pt là: x- y – 5= 0.
=> Đường thẳng AB có pt là: x- y – 5= 0.
Gọi G(a;3a- 8) suy ra C( 3a- 5; 9a -19).
Ta có:

Vậy C( 1 ; -1) và C( -2 ; 10)

a, Gọi \(I\left(x;y\right)\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}IA=IB\\IA=IC\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}IA^2=IB^2\\IA^2=IC^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-3-x\right)^2+\left(6-y\right)^2=\left(1-x\right)^2+\left(-2-y\right)^2\\\left(-3-x\right)^2+\left(6-y\right)^2=\left(6-x\right)^2+\left(3-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2y=-5\\3x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)

Cho hình vẽ
Tam giác BEC cân và có \(\widehat{BEC}=150^o\) \(\Rightarrow\) tam giác BEC cân tại E
Gọi H là hình chiếu của E lên AD \(\Rightarrow\) H là trung điểm AD và HE \(=\) d E; AD \(=\) 3
Đặt cạnh hình vuông là \(AB=x\)
Tam giác BEC cân tại E có \(\widehat{BEC}=150^o\Rightarrow\widehat{BEC}=15^o\) . Gọi I là trung điểm của \(BC\Rightarrow BI=\frac{x}{2};EI=x-3\)
Tam giác BIE vuông tại I có góc \(\widehat{EBI}=15^o\Rightarrow tan15^o=\frac{EI}{BI}=\frac{2x-6}{x}\)
\(\Rightarrow2-\sqrt{3}=\frac{2x-6}{x}\Leftrightarrow x=2\sqrt{3}\)
Phương trình đường thẳng EH qua điểm E và vuông góc với \(AD\Rightarrow EH\div4x+3y+4=0\)
Đường thằng \(AB\\ EH\Rightarrow AB\) có dạng \(''d''\div4x+3y+a=0\)
Ta có d \(''E,AB''=\frac{⊥a-4⊥}{5}=BI=\sqrt{3}\Leftrightarrow a=4⊥5\sqrt{3}\)
Phương trình đường thẳng AB là \(''d''\div4x+3y+4⊥5\sqrt{3}=0\)
P/s; Bộ khó lắm à .
Do O là trung điểm AC \(\Rightarrow\left\{{}\begin{matrix}x_O=\frac{x_A+x_C}{2}\\y_O=\frac{y_A+y_C}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=-x_A=-3\\y_C=-y_A=-1\end{matrix}\right.\)
Tương tự: \(\left\{{}\begin{matrix}x_D=-x_B=-1\\y_D=-y_B=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}C\left(-3;-1\right)\\D\left(-1;-2\right)\end{matrix}\right.\)
b/ Ta có \(\overrightarrow{AB}=\left(-2;1\right)\Rightarrow\) đường thẳng AB nhận \(\overrightarrow{n_{AB}}=\left(1;2\right)\) là 1 vtpt
Phương trình AB:
\(1\left(x-3\right)+2\left(y-1\right)=0\Leftrightarrow x+2y-5=0\)
\(\overrightarrow{DA}=\left(4;3\right)\Rightarrow\) đường thẳng AD nhận \(\overrightarrow{n}=\left(3;-4\right)\) là 1 vtpt
Phương trình AD:
\(3\left(x-3\right)-4\left(y-1\right)=0\Rightarrow3x-4y-5=0\)
Hai cạnh còn lại bạn tự viết tương tự