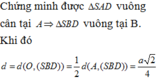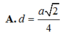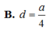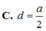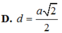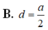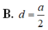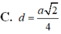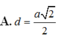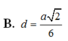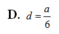cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy lớn là AB. Biết AD=DC=CB=a, AB=2a, SA vuông góc với đáy, mặt phẳng (SBD) tạo với đáy 1 góc 45 độ. Gọi I là trung điểm cạnh AB. Tính khoảng cách từ I đến mặt phẳng (SBD).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 4 2019
Chọn C
Phương pháp:
- Xác định góc giữa mặt phẳng (SBD) với (ABD) (góc giữa hai đường thẳng cùng vuông góc với giao tuyến)
- Tính khoảng cách dựa vào công thức tỉ số khoảng cách:
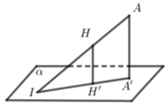
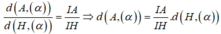
Cách giải
CM
23 tháng 8 2019
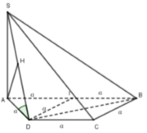
Chọn B
Chứng minh được ∆ S A D vuông cân tại A và ∆ A B D vuông tại D.
Khi đó d G , S B D = 1 3 d A , S B D = a 2 6 .
22 tháng 2 2021
Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
23 tháng 2 2021
.jpg)
là trọng tâm tam giác SAE.
Tứ diện AEND vuông tại đỉnh A nên
Vậy
CM
7 tháng 12 2017
Đáp án C
Theo dữ kiện đề bài cho, dễ dàng chứng minh được ΔACD vuông tại cân C và A C = A D 2 = a 2 .
C D ⊥ A C C D ⊥ S A ⇒ C D ⊥ S A C ⇒ S A C ⊥ S C D
Mà S A C ∩ S C D = S C , từ A kẻ A H ⊥ S C . Khi đó d A ; S C D = A H .
Tam giác SAC vuông tại
A: 1 A H 2 = 1 S A 2 + 1 A C 2 = 1 a 2 + 1 2 a 2 = 3 2 a 2 ⇒ d A ; S C D = A H = a 2 3
Mặt khác: A D ∩ S C D = D và M là trung điểm AD nên:
d M ; S C D d A ; S C D = M D A D = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C D = a 6 6
HN
9 tháng 3 2022
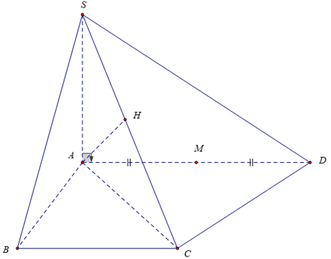
Gọi E là trung điểm AB, ta có đáy tạo bởi ba tam giác đều ADE, DEC, CEB.
Suy ra, góc ADE bằng 60o, góc EDB bằng 30o.
Suy ra, tam giác ADB và SDB là hai tam giác vuông tại D.
Suy ra, góc tạo bởi (SBD) và đáy ABCD là góc SDA với độ lớn 45o.
Suy ra, SA=a.
d(C,(SBD))=d(E,(SBD))=(1/2).d(A,(SBD))=(1/2).a\(\sqrt{2}\)/2=a\(\sqrt{2}\)/4.
CM
26 tháng 5 2019
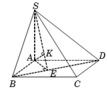
Xác định
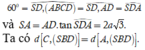
Tam giác vuông BAD có 
Tam giác vuông SAE có 
Chọn A.
