h elp bai 2
elp bai 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 2:
a, Kẻ Ez//Cx//AB
DO đó \(\widehat{BAE}=\widehat{AEz}=40^0\Rightarrow\widehat{CEz}=\widehat{AEC}-\widehat{AEz}=60^0-40^0=20^0\)
Mà Cx//Ez nên \(\widehat{CEz}=\widehat{ECx}=20^0\left(so.le.trong\right)\)
b, Ta có \(\widehat{CEM}=180^0-\widehat{AEC}=120^0\left(kề.bù\right)\)
Vì AB//Cx nên \(\widehat{ABE}=\widehat{CME}=40^0\left(so.le.trong\right)\)
Kẻ thêm đoạn thẳng IL sao cho IL//AB//Cx và IL cắt điểm E
a) Ta có: góc AEI = góc BAE = 40 độ ( so le trong, IL//AB)
Ta có: góc AEI + góc CEI = góc AEC = 60 độ
hay : 40 độ + góc CEI = 60 độ
=> góc CEI = 60 độ - 40 độ = 20 độ
Ta lại có: góc CEI = góc ECx = 20 độ ( sole trong và IL//Cx)

1 ngày có số giây là
24 x 60 x 60 = 86400 (giay)
co so o to di qua la
86400 : 50 = 1728 ô tô
t5k va kbv nha
đổi 1 ngày = 24 giờ = 86400 giây
trong một ngày có số lượt ô tô chạy qua cầu là:
86400 : 50 = 1728 lượt
đáp số 1728 lượt

Câu 3.
Diện tích xung quanh là:
( 4+3,5)×2×3=45(métvuong)
Dt toàn phần là:
(4×3,5)+45=59(met vuong)
Thời gian quét xi măng là:
59×15=88,5 phút
Ds:88,5 phút
4: c

Mở bài : có nhiệm vụ nêu ra chủ đề của văn bản .
Thân bài : thường có 1 số đoạn nhỏ trình bày khía cạnh của chủ đề .
Kết bài : tổng kết chủ đề của văn bản
Nội dung phần thân bài : được trình bày theo trình tự tùy thuộc vào kiểu văn bản , chủ đề , ý đồ của người viết . Nội dung ấy thường đk sắp xếp theo trình tự thời gian và ko gian , theo sự phát triển của sự việc hay theo mạch suy luận , sao cho phù hợp với sự triển khai chủ đề và sự tiếp nhân của người đọc .
vì bạn ra đề bài ko rõ , nên mk nghĩ chắc bạn hỏi cái này

a) Ta có: DE//AB
\(\Rightarrow\widehat{BAC}=\widehat{AED}=60^0\)(so le trong)
\(\Rightarrow\widehat{DEC}=180^0-\widehat{AED}=180^0-60^0=120^0\)(kề bù)
b) Kẻ Cy//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACy}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{ACF}+\widehat{FCy}+\widehat{BAC}=180^0\)
\(\Rightarrow\widehat{FCy}=180^0-60^0-40^0=80^0\)
\(\Rightarrow\widehat{FCy}+\widehat{CFG}=80^0+100^0=180^0\)
Mà 2 góc này trong cùng phía
=> Cy//FG
Mà FG//AB//DE
=> DE//FG
12.
a,Vì DE//AB nên \(\widehat{DEA}=\widehat{EAB}=60^0\)
\(\Rightarrow\widehat{DEC}=180^0-\widehat{DEA}=120^0\left(kề.bù\right)\)
b, Kẻ xy//DE//AB (C∈xy)
\(\Rightarrow\widehat{BAC}=\widehat{ECx}=60^0\left(so.le.trong\right)\\ \Rightarrow\widehat{FCy}=180^0-\widehat{ACF}-\widehat{ACx}=180^0-60^0-40^0=80^0\left(kề.bù\right)\\ \Rightarrow\widehat{FCy}+\widehat{CFG}=80^0+100^0=180^0\)
Mà 2 góc này ở vị trí trong cùng phía nên xy//FG
Mà xy//DE nên DE//FG

bài 48
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy
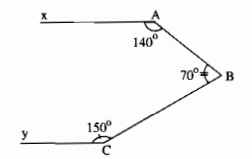
Giải
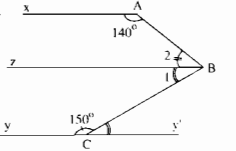
Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy
bài 49
Hình dưới cho biết ˆA=140∘;ˆB=70∘;ˆC=150∘A^=140∘;B^=70∘;C^=150∘
Chứng minh rằng Ax // Cy

Giải

Kẻ tia Bz // Ax và Cy’ là tia đối của tia Cy
Ta có: ˆB2+ˆxAB=180∘B2^+xAB^=180∘ (hai góc trong cùng phía)
Mà ˆxAB=140∘(gt)xAB^=140∘(gt)
Suy ra: ˆB2=180∘−ˆxABB2^=180∘−xAB^
⇒⇒ ˆB2=180∘−140∘=40∘B2^=180∘−140∘=40∘
Mà ˆB1+ˆB2=ˆABCB1^+B2^=ABC^
⇒ˆB1=ˆABC−ˆB2⇒B1^=ABC^−B2^
= 70° - 40° = 30° (1)
ˆyCB+ˆBCy′=180∘yCB^+BCy′^=180∘ (2 góc kề bù)
⇒ˆBCy′=180∘−ˆyCB=180∘−150∘=30∘(2)⇒BCy′^=180∘−yCB^=180∘−150∘=30∘(2)
Từ (1) và (2) suy ra: ˆB1=ˆBCy′B1^=BCy′^
Suy ra: Cy’ // Bz (Vì có cặp góc ở vị trí so le trong bằng nhau)
Hay Cy // Bz mà Bz // Ax suy ra l ; Ax // Cy