Bài tập :
B1 Viết phương trình đường tròn (C1) có bán kính R1 = 1 , tiếp xúc với trục Ox và có tâm nằm trên đường thẳng denta : 3x - y +7 = 0
B2 Cho đường tròn (C) : x2 + y2 - 2x - 4y - 4 = 0 và đường thẳng (d) : 3x + 4y +4 = 0 . Chứng minh rằng (d) tiếp xúc với (C)

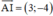 là một vtpt và đi qua A(–1; 0)
là một vtpt và đi qua A(–1; 0)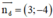 là một vtpt; 1 VTCP là
là một vtpt; 1 VTCP là 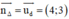 là một vtpt
là một vtpt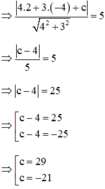

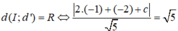
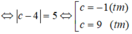
Bài 1:
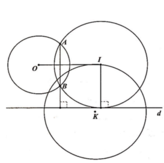
Gọi $I$ là tâm đường tròn. Vì $I$ nằm trên đt \(\Delta: 3x-y+7=0\) nên $I$ có tọa độ $(a,3a+7)$
Đường tròn tiếp xúc với trục Ox nên:
\(d(I,Ox)=R=1\Leftrightarrow |3a+7|=1\Rightarrow \left[\begin{matrix} a=-2\\ a=\frac{-8}{3}\end{matrix}\right.\)
Nếu \(a=-2\Rightarrow I(-2, 1)\). PTĐTr là:
\((x+2)^2+(y-1)^2=1\)
Nếu \(a=-\frac{8}{3}\Rightarrow I(\frac{-8}{3}, -1)\). PTĐTr là:
\((x+\frac{8}{3})^2+(y+1)^2=1\)
Bài 2:
Ta viết lại pt đường tròn:
\(x^2+y^2-2x-4y-4=0\)
\(\Leftrightarrow (x-1)^2+(y-2)^2-9=0\)
\(\Leftrightarrow (x-1)^2+(y-2)^2=9\)
Vậy đường tròn $(C)$ có tâm $I(1,2)$ và bán kính $R=3$
Có : \(d(I,(d))=\frac{|3x_I+4y_I+4|}{\sqrt{3^2+4^2}}=\frac{|3.1+4.2+4|}{5}=3=R_{(C)}\)
Do đó đường thẳng (d) tiếp xúc với đường tròn $(C)$