Xét một bộ bài 52 lá. Nếu những lá bài này được đánh dấu bằng các số nguyên khác nhau, hỏi xác suất để các lá bài này được sắp xếp theo một dãy số nguyên tăng dần là bao nhiêu ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi đặt tụ 19 lá dưới tụ còn lại thì lá bài của đối phương sẽ là lá bài thứ 34 (tụ ở trên có 33 lá)
nếu theo khả năng 2 : đếm đến 1 mà số đếm vẫn khác....... thì số bài đã lấy ra sẽ đúng 33 lá
Khi đó lá bài tiếp theo (úp) sẽ là lá bài của đối phương : lá thứ 34.
p/s: làm thử 1 trường hợp vì không chắc .-.

Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá bích n(A) = 13
Suy ra 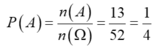
Chọn B.

Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá át n(A)=4
Suy ra 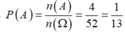
Chọn C.

Số phần tử không gian mẫu: n(Ω)=52
Số phần tử của biến cố xuất hiện lá J đỏ hay lá 5 là n(A)=2+4=6
Suy ra 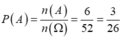
Chọn B.

Số phần tử không gian mẫu: n(Ω) = 52
Số phần tử của biến cố xuất hiện lá át hay lá rô n(A) = 4 +12 = 16.
Suy ra 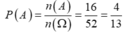
Chọn C.

Gọi A là biến cố "Rút được 2 lá bài cơ".
Số kết quả thuận lợi là \(\left|\Omega_A\right|=C^2_{13}=78\).
Số kết quả có thể xảy ra là \(\left|\Omega\right|=C^2_{52}=1326\).
\(\Rightarrow\) Xác suất xảy ra biến cố A là \(P\left(A\right)=\dfrac{78}{1326}=\dfrac{1}{17}\).

uses crt;
var a:array[1..1000]of integer;
i,n,j,tam,t,t1,tam,dem,max:integer;
begin
clrscr;
n:=0;
t:=0;
repeat
inc(n);
write('A[',n,']='); readln(a[n]);
t:=t+a[n];
until t>100;
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
writeln('Day so theo chieu tang dan la: ');
for i:=1 to n do
write(a[i]:4);
writeln;
t1:=0;
dem:=0;
for i:=1 to n do
if a[i] mod 3=0 then
begin
t1:=t1+a[i];
inc(dem);
end;
max:=a[1];
for i:=1 to n do
if max<a[i] then max:=a[i];
writeln('Tong cac so la boi cua 3 la: ',t1);
writeln('So lon nhat cua day la: ',max);
writeln('So luong so la boi cua 3 la: ',dem);
readln;
end.
1/5200