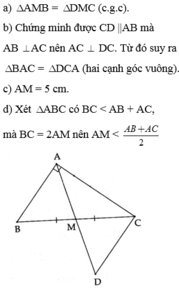
Cho tam giác ABC có AB = AC = 5cm, BC = 6cm, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA
a) Tính AM
b) Chứng minh tam giác ABM = tam giác DCM
c) Chứng minh tam giác ACD cân
d) Gọi I là trung điểm của BM. Trên tia đối của tia IA lấy điểm K sao cho I là trung điểm của AK. KC cắt AD tại E. Chứng minh ED = \(\frac{1}{4}\)AD