Tìm tất cả các số nguyên tố p sao cho \(p^2-p+1\) là lập phương của một số tự nhiên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
9 tháng 3 2021
Giả sử tồn tại số \(p\)thỏa mãn.
Ta đặt \(\frac{p^2-p-2}{2}=a^3\).
- \(p=2\)thỏa mãn.
- \(p>2\)do là số nguyên tố nên \(p\)lẻ.
Ta có: \(\frac{p^2-p-2}{2}=a^3\Leftrightarrow p\left(p-1\right)=2\left(a+1\right)\left(a^2-a+1\right)\)suy ra \(p\)là ước của \(a+1\)hoặc \(a^2-a+1\).
+) \(p|a+1\): \(\frac{p^2-p-2}{2}=a^3\)suy ra \(a< p\Rightarrow a+1=p\).
Thế vào cách đặt ban đầu ta được \(\frac{\left(a+1\right)^2-\left(a+1\right)-2}{2}=a^3\Leftrightarrow2a^3-a^2-a+2=0\)
\(\Leftrightarrow a=-1\)không thỏa.
+) \(p|a^2-a+1\): Đặt \(a^2-a+1=kp\)(1).
\(p\left(p-1\right)=2\left(a+1\right)\left(a^2-a+1\right)=2\left(a+1\right)kp\)
\(\Rightarrow p-1=2\left(a+1\right)k\Leftrightarrow p=2k\left(a+1\right)+1\)thế vào (1):
\(a^2-a+1=k\left[2k\left(a+1\right)+1\right]\)
\(\Leftrightarrow a^2-\left(2k^2+1\right)a-2k^2-k+1=0\)
\(\Delta=\left(2k^2+1\right)^2-4\left(-2k^2-k+1\right)=4k^4+12k^2+4k-3\).
Ta cần tìm số tự nhiên \(k\)để \(\Delta\)là số chính phương.
Ta có: \(4k^4+12k^2+4k-3>4k^4+8k^2+4=\left(2k^2+2\right)^2\)
\(4k^4+12k^2+4k-3< 4k^4+16k^2+16=\left(2k^2+4\right)^2\)
Theo nguyên lí kẹp suy ra \(4k^4+12k^2+4k-3=\left(2k^2+3\right)^2\)
\(\Leftrightarrow4k-3=9\Leftrightarrow k=3\).
Với \(k=3\): \(a^2-19a-20=0\Rightarrow a=20\Rightarrow p=127\).
Vậy \(p\in\left\{2,127\right\}\).
AD
0
22 tháng 4 2018
2,Giải:
♣ Ta thấy p = 2 thì 2p + 1 = 5 không thỏa = n³
♣ Nếu p > 2 => p lẻ (Do Số nguyên tố chẵn duy nhất là 2 )
Mặt khác : 2p + 1 là 1 số lẻ => n³ là một số lẻ => n là một số lẻ
=> 2p + 1 = (2k + 1)³ ( với n = 2k + 1 )
<=> 2p + 1 = 8k³ + 12k² + 6k + 1
<=> p = k(4k² + 6k + 3)
=> p chia hết cho k
=> k là ước số của số nguyên tố p.
Do p là số nguyên tố nên k = 1 hoặc k = p
♫ Khi k = 1
=> p = (4.1² + 6.1 + 3) = 13 (nhận)
♫ Khi k = p
=> (4k² + 6k + 3) = (4p² + 6p + 3) = 1
Do p > 2 => (4p² + 6p + 3) > 2 > 1
=> không có giá trị p nào thỏa.
Đáp số : p = 13
NN
1
14 tháng 2 2021
Đặt \(13p+1=n^3\left(n\in N\right)\)
\(\Leftrightarrow13p=n^3-1\)
\(\Leftrightarrow13p=\left(n-1\right)\left(n^2+n+1\right)\)
Trường hợp 1: \(n-1=13\forall n^2+n+1=p\)
\(\Leftrightarrow n=14\)
hay \(p=14^2+14+1=196+14+1=211\)(nhận)
Trường hợp 2: \(n-1=p\forall n^2+n+1=p\)
\(\Leftrightarrow n^2+2=13-p\)
\(\Leftrightarrow\left(p+1\right)^2=11-p\)
\(\Leftrightarrow p=2\)(nhận)
Vậy: \(p\in\left\{2;211\right\}\)
CM
15 tháng 7 2017
1.Với a = 2 ta có 2a + 1 = 5 không thích hợp
Với a ≠ 2 do a là số nguyên tố nên a lẽ
Vậy 2a + 1 là lập phương của một số lẽ nghĩa là
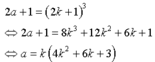
Từ đó k là ước của a. Do k là số nguyên tố nên k = 1 hoặc k = a
-Nếu k = 1 thì 2a + 1 = (2.1 + 1)3 suy ra a = 13 thớch hợp
- Nếu a = k từ a = a(4a2 + 6a + 3) do a là nguyên tố nên suy ra
1 = 4a2 + 6a + 3 không có số nguyên tố a nào thoả món phương trỡnh này Vì vế phải luụn lớn hơn 1
Vậy a = 13
2.Giả sử
13 và p là các số nguyên tố , mà n – 1 > 1 và n2 + n + 1 > 1
Nên n – 1 = 13 hoặc n – 1 = p
- Với n – 1 =13 thì n = 14 khi đó 13p = n3 – 1 = 2743 suy ta p = 211 là số nguyên tố
- Với n – 1 = p thi n2 + n + 1 = 13 suy ra n = 3 . Khi đó p = 2 là số nguyên tố
Vậy p = 2, p = 211 thì 13p + 1 là lập phương của một số tự nhiên
OO
1
7 tháng 5 2020
Đặt 7p + 1 = n^3 (n > 2)
=> 7p = (n - 1)(n^2 + n + 1)
Ta có 2 TH :
TH1 : n - 1 = 7 \(\forall\)n^2 + n +1 = p => n = 8 => p = 73
TH2 : n - 1 = p \(\forall\) n^2 + n + 1 =7 => ....
