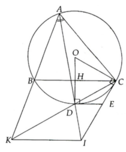
Cho đường tròn (O,R) với dây BC cố định. điểm A thuộc cung lớn BC .đường phân giác của góc BAC cắt đường tròn O tại D. các tiếp tuyến của đường tròn O tại C và D cắt nhau tại E. tia CD cắt AB tại K ,đường thẳng AD cắt CE tại I
1.Tìm vị trí của A trên cung lớn BC để diện tích tứ giác ABDC lớn nhất
2.AD cắt BC tại M , Chứng minh AB.AC = AM2 + MB.MC