Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

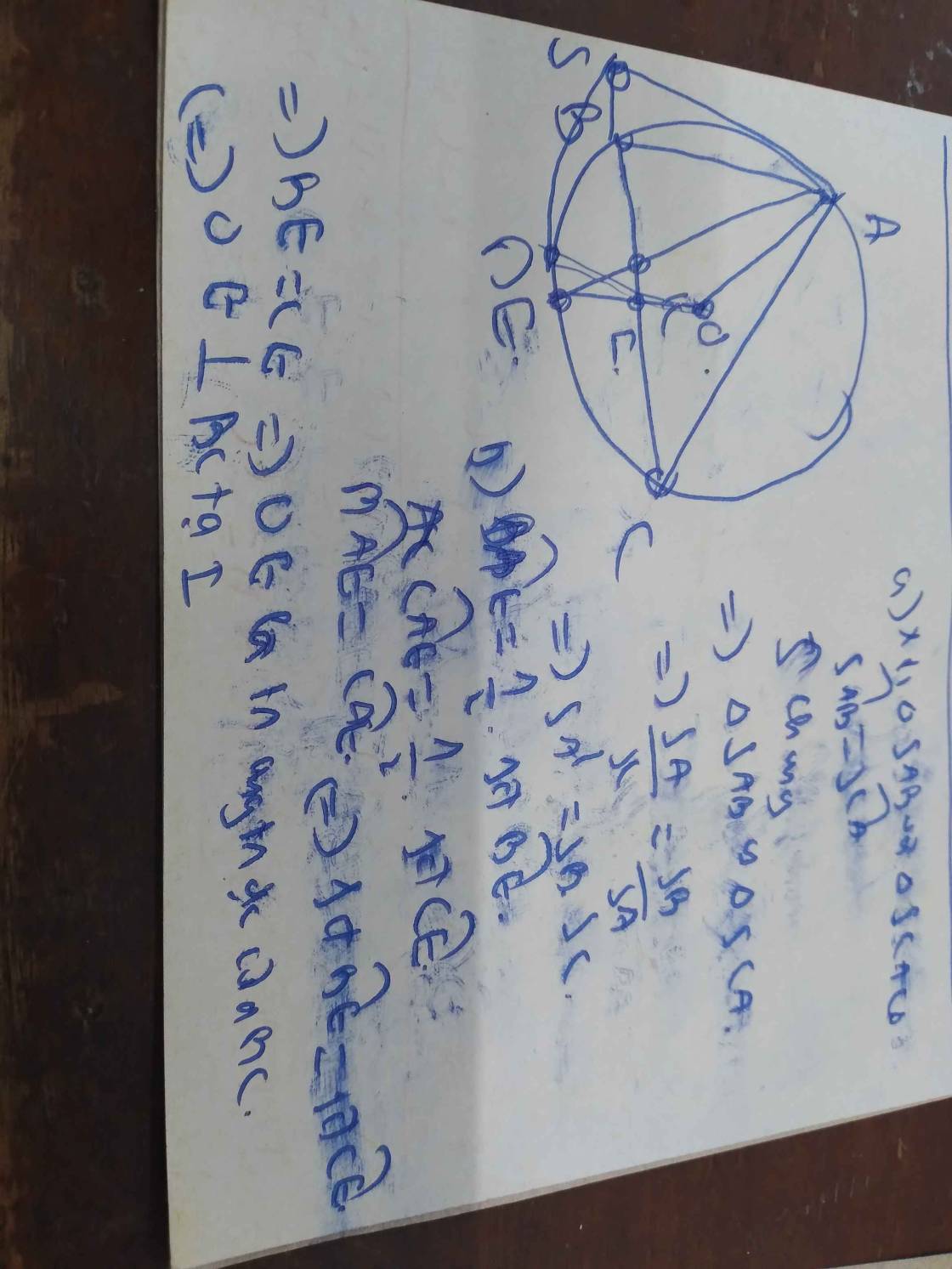
a, AD là phân giác B A C ^
=> D là điểm chính giữa B C ⏜ => OD ⊥ BC
Mà DE là tiếp tuyến => ĐPCM
b, E C D ^ = 1 2 s đ C D ⏜ = D A C ^ = B A D ^ => Đpcm
c, HC = P 3 2 => H O C ^ = 60 0 => B O C ^ = 120 0
=> l B C ⏜ = π . R . 120 0 180 0 = 2 3 πR

a) vì AD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAD}=\widehat{DAC}\)\(\Rightarrow\)D là điểm chính giữa BC
\(\Rightarrow OD\perp BC\)
Mà \(DE\perp OD\)
\(\Rightarrow BC//DE\)
b) Ta có : \(\widehat{DAC}=\widehat{DCI}=\frac{1}{2}sđ\widebat{CD}\)
\(\Rightarrow\widehat{KAD}=\widehat{KCI}\)
suy ra tứ giác ACIK nội tiếp
c) OD cắt BC tại H
Dễ thấy H là trung điểm BC nên HC = \(\frac{BC}{2}=\frac{\sqrt{3}}{2}R\)
Xét \(\Delta OHC\)vuông tại H có :
\(HC=OC.\sin\widehat{HOC}\Rightarrow\sin\widehat{HOC}=\frac{HC}{OC}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{HOC}=60^o\)
\(\Rightarrow\widehat{BOC}=120^o\)
\(\Rightarrow\widebat{BC}=120^o\)
P/s : câu cuối là tính số đo cung nhỏ BC mà sao có cái theo R. mình ko hiểu. thôi thì bạn cứ xem đi nha.

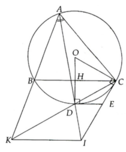
c) Gọi T là giao điểm thứ hai của FD với đường tròn (O). Ta c/m EO đi qua T.
Ta có: ^ADM = ^DAC + ^DCA = ^BAC/2 + ^ACB = ^BAD + ^MAB = ^MAD => \(\Delta\)DAM cân tại M => MA=MD
Lại có: MA và MF là 2 tiếp tuyến của (O) nên MA=MF. Do đó: MD=MF => \(\Delta\)MDF cân tại M (đpcm).
Dễ thấy: \(\Delta\)MAB ~ \(\Delta\)MCA (g.g) và \(\Delta\)MFB ~ \(\Delta\)MCF (g.g)
=> \(\frac{MA}{MC}=\frac{MF}{MC}=\frac{AB}{AC}=\frac{BD}{CD}=\frac{FB}{FC}\) => FD là tia phân giác ^BFC (1)
Kẻ tia đối Fy của FB => ^EFy = ^ECB = ^EBC = ^EFC => FE là phân giác ^CFy (2)
Từ (1) và (2) suy ra: FD vuông góc với FE (Vì ^BFC + ^CFy = 1800) hay ^EFT = 900
=> ET là đường kính của (O) => ET trùng với OE => OE đi qua T => ĐPCM.
d) Áp dụng ĐL Ptolemy có tứ giác BFCT nội tiếp có: BF.CT + CF.BT = BC.FT
=> CT.(BF+CF) = BC.FT => \(BF+CF=\frac{BC.FT}{CT}\le\frac{BC.ET}{CT}=\frac{2CK.ET}{CT}=2EC=2BE\)
Dấu "=" xảy ra khi F trùng với E <=> MF vuông góc OE <=> MF // BC => M không nằm trên BC (mâu thuẫn)
=> Không có dấu "=" => BF+CF < 2BE (đpcm).