Question

[Thăng Vũ]

Cho tam giác ABC nhọn nội tiếp đường tròn (O).H là trực tâm của tam giác ABC,AD là đường kính của (O).,E thuộc AC sao cho HE song song với BC.

a,CMR các đường thẳng BH,DE cắt nhau tại 1 điểm thuộc đường tròn (O). 

b,Gọi F là giao điểm của EH và AB.CMR A thuộc đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF. 

c,Gọi I là tâm đường tròn nội tiếp tam giác DEF.CMR các đường thẳng BE,CF,IH đồng quy

Giúp mình câu c với

Answer 1

[Nguyễn Tất Đạt]

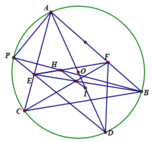
a) Gọi BH cắt (O) tại S khác B. Qua tính chất quen thuộc của trực tâm  ta thấy H,S đối xứng nhau qua AC.

Do đó ^ASE = ^AHE = 90⁰ (Vì HE // BC, AH vuông góc BC) hay SE vuông góc với AS (1)

Ta có AD là đường kính của (O) => ^ASD chắn nửa (O) => SD vuông góc với AS (2)

Từ (1) và (2) suy ra SE trùng SD hay DE cắt (O) tại S. Như vậy BH,DE cắt nhau trên (O) (đpcm).

b) Tương tự câu a, CH,DF cũng cắt nhau tại 1 điểm trên (O), gọi nó là T

Dễ thấy AH = AS = AT (Tính chất đối xứng). Mà AH,AS,AT lần lượt là khoảng cách từ A đến EF,DE,DF

Nên A chính là tâm bàng tiếp góc D của \(\Delta\)DEF (A nằm ngoài \(\Delta\)DEF) (đpcm).

c) Gọi IH cắt CF tại G. Ta sẽ chỉ ra rằng B,G,E thẳng hàng. Thật vậy:

Ta có FA,FI là phân giác trong và ngoài của ^DFE => FI vuông góc AB => FI // CH

Từ đó \(\Delta\)IGF ~ \(\Delta\)HGC (g.g) => \(\frac{GI}{GH}=\frac{IF}{HC}\)(3)

Mặt khác ^IFE = ^FAH (Cùng phụ ^AFH) = ^HCB. Tương tự ^IEF = ^HBC

Suy ra \(\Delta\)EIF ~ \(\Delta\)BHC (g.g) => \(\frac{IF}{HC}=\frac{IE}{HB}\)(4)

Từ (3) và (4), kết hợp với ^GIE = ^GHB suy ra \(\Delta\)GEI ~ \(\Delta\)GBH (c.g.c)

=> ^IGE = ^HGB. Vì I,G,H thẳng hàng nên kéo theo B,G,E thẳng hàng

Vậy thì BE,CF,IH cắt nhau tại G (đpcm).

Answer 2

[Nguyễn Xuân Trường]

Bạn ơi, chứng minh cho mình câu b: AH=AS=AT với được không ạ