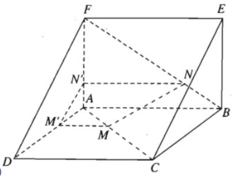
cho 2 hình vuông ABCD, ABEF không đồng phẳng. Trên AC, BF lấy 2 điểm M, N sao cho AM= BN. Các đườngsong song với AB vẽ từ M, N lần lượt cắt AD; AF tại M',N'.
Gọi I là trung điểm MN tìm tập hợp điểm I khi M,N di động
(Giúp Mình Với)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
13 tháng 12 2020
Nghĩ ra hướng làm rồi cơ mà giờ "bỗng dưng bận" nên để lát nữa tui "múa bút" nhó ahehe :3
HT
13 tháng 12 2020
Mà viết thử hướng làm cho bà nghĩ coi sao.
Phần bài ũy tích thì sẽ chứng minh theo 2 phần là phần đảo và phần thuận
Phần thuân: Có I là trung điểm MN thì chứng minh khi M, N di động thì I sẽ di động trên đường thẳng HK (H là TD AB, K là trung điểm FC)
Phần đảo: Có I thuộc HK, chứng minh tồn tại 2 điểm M thuộc AC, N thuộc BF sao cho AM=BN và nhận I làm trung điểm MN
Đó, nghĩ thử đi đã :3
CM
4 tháng 1 2019
a)
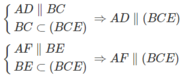
Mà AD, AF ⊂ (ADF)
Nên (ADF) // (BCE)
b) Vì ABCD và ABEF là các hình vuông nên AC = BF. Ta có:
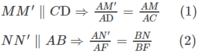
So sánh (1) và (2) ta được:
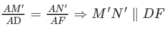
c) Từ chứng minh trên suy ra DF // (MM′N′N)
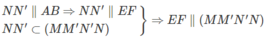
Mà DF,EF ⊂ (DEF) nên (DEF) // (MM′N′N)
Vì MN ⊂ (MM′N′N) và (MM′N′N) // (DEF) nên MN // (DEF).
CM
17 tháng 9 2017
MN // DE nên DM, NE cắt nhau tại điểm I và
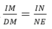
Lại có
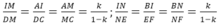
Mặt khác:
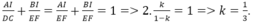
Đáp án A.
Viết lại đề cho tử tế đi bạn, các điểm E, M', N' xuất hiện trên đời có ý nghĩa gì vậy ạ?
Toán lớp 11 bạn ơi bạn học lớp mấy ?