cho hàm số y = x^2 - 2x - 3(P) và y = x - 3(d). Gọi A và B theo thứ tự là giao điểm của (d) và (P). Tìm tọa độ điểm M thuộc trục đối xứng của (P) sao cho | MA + MB | đạt giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 7 2017
a) Vẽ đồ thị
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = . (-1,5)2 =
. 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 =
. 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.
1 tháng 12 2019
1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)
b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5
Thay y=5 và x=0 vào hs và tìm k
2. a) Tự vẽ
b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)
c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y) (x=-2; y=0)
3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)
Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1
Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3
4 tháng 4 2017
a) Vẽ đồ thị
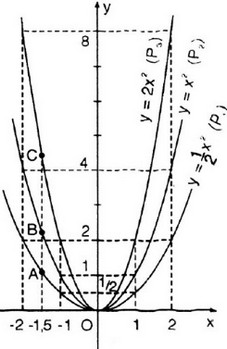
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = 
. (-1,5)2 = . 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 = . 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.
2
13 tháng 1 2023
Gọi `M(x;3/2x+5/2)`
Ta có:`|\vec{MA}-2\vec{MB}|`
`=|(4-x;7-3/2x-5/2)-2(2-x;1-3/2x-5/2)|`
`=|(x;3/2x+17/2)|`
`=\sqrt{x^2+(3/2x+17/2)^2}`
`=\sqrt{x^2+9/4x^2+51/2x+289/4}`
`=\sqrt{13/4x^2+51/2x+289/4}`
`=\sqrt{(\sqrt{13}/2 x+[51\sqrt{13}]/26)^2+289/13} >= [17\sqrt{13}]/13`
Dấu "`=`" xảy ra `<=>\sqrt{13}/2x+[51\sqrt{13}]/26=0<=>x=-51/13`
`=>M(-51/13;-44/13)`
26 tháng 2 2022
b: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\0.5x+2=0\end{matrix}\right.\Leftrightarrow A\left(-4;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}y_B=0\\5-2x_B=0\end{matrix}\right.\Leftrightarrow B\left(2.5;0\right)\)
Tọa độ điểm C là:
\(\left\{{}\begin{matrix}0.5x+2=5-2x\\y=-2x+5\end{matrix}\right.\Leftrightarrow C\left(1.2;2.6\right)\)
c: \(AB=6.5\)
\(BC=\sqrt{\left(1.2-2.5\right)^2+2.6^2}=\dfrac{13\sqrt{5}}{10}\)
\(AC=\sqrt{\left(1.2+4\right)^2+2.6^2}=\dfrac{13\sqrt{5}}{5}\)
Vì \(AC^2+BC^2=AB^2\) nên ΔABC vuông tại C
\(C=6.5+\dfrac{13\sqrt{5}}{10}+\dfrac{13\sqrt{5}}{5}=\dfrac{65+39\sqrt{5}}{10}\)
\(S=\dfrac{13\sqrt{5}}{10}\cdot\dfrac{13\sqrt{5}}{5}=16.9\)
