Tìm số nguyên a để hai phương trình sau có nghiệm chung:
\(x^2+ax+8=0\)
\(x^2+x+a=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\left(x-2\right)\left(x^2-7x+41\right)=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Thay x=2 vào (2), ta được:
\(2^2-2m+m^2-5m+8=0\)
\(\Leftrightarrow m^2-7m+12=0\)
\(\Leftrightarrow\left(m-3\right)\left(m-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=3\\m=4\end{matrix}\right.\)
Vậy: Có 2 giá trị nguyên của m thỏa mãn hai phương trình có nghiệm chung


Ý tưởng như sau:
\(x^2+ax+1=0\) và \(x^2+bx+c=0\) là 2 pt có nghiệm chung nên hệ pt sau có nghiệm (nhận xét quan trọng):
\(\hept{\begin{cases}x^2+ax+1=0\\x^2+bx+c=0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(a-b\right)x=c-1\\x^2+ax+1=0\end{cases}}\)
Do \(a\ne b\) nên thay \(x=\frac{c-1}{a-b}\) xuống pt dưới được: \(\left(\frac{c-1}{a-b}\right)^2+\frac{a\left(c-1\right)}{a-b}+1=0\)
Hay \(\left(c-1\right)^2+a\left(c-1\right)\left(a-b\right)+\left(a-b\right)^2=0\)
-----
\(x^2+x+a=0\) và \(x^2+cx+b=0\) có nghiệm chung thì hệ pt sau có nghiệm:
\(\hept{\begin{cases}x^2+x+a=0\\x^2+cx+b=0\end{cases}\Leftrightarrow\hept{\begin{cases}\left(c-1\right)x=a-b\\x^2+x+a=0\end{cases}}}\)
Do \(a\ne b\) nên \(c\ne1\), thay \(x=\frac{a-b}{c-1}\) xuống pt dưới được:
\(\left(\frac{a-b}{c-1}\right)^2+\frac{a-b}{c-1}+a=0\) hay \(\left(a-b\right)^2+\left(a-b\right)\left(c-1\right)+a\left(c-1\right)^2=0\)
-----
Đặt \(x=a-b,y=c-1\)
Ta có hệ: \(\hept{\begin{cases}x^2+axy+y^2=0\\x^2+xy+ay^2=0\end{cases}\Rightarrow\left(a-1\right)xy=\left(a-1\right)y^2}\)
Nhớ rằng \(a=1\) không xảy ra vì khi đó \(x^2+ax+1=0\) vô nghiệm.
Vậy \(a\ne1\), do \(y\ne0\) nên \(x=y\). Tức là \(a-b=c-1\).
Tới đây quay lại mấy cái nghiệm chung sẽ thấy các nghiệm chung đều là \(1\).
Mà như vậy thì \(b+c=-1,a=-2\) nên \(a+b+c=-4\)

Chọn đáp án B
Gọi x 0 là nghiệm thực chung của 2 phương trình
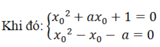
⇒ x 0 2 + a x 0 + 1 = x 0 2 - x 0 - a ⇔ (a + 1) x 0 = -(a + 1) ⇔ x 0 = -1
Thay x 0 = -1 vào phương trình x 0 2 + a x 0 + 1 = 0 tìm được a = 2

\(x^3+3x^2+2x=0\Rightarrow x\left(x+1\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=-2\end{matrix}\right.\)
\(\left(x+1\right)\left(x^2+2x+1+a\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+1=-a\end{matrix}\right.\)
Vì 2 pt đã có nghiệm chung là \(-1\Rightarrow\) nghiệm của pt \(\left(x+1\right)^2=-a\) phải khác \(0,2\)
\(\Rightarrow a\ne-1;-9\)
(cách mình là vậy chứ mình cũng ko chắc là có đúng ko nữa)

a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có đúng k bn

Gọi m là nghiệm chung của 2 phương trình thì ta có:
\(\hept{\begin{cases}m^2+am+6=0\\m^2+bm+12=0\end{cases}}\)
\(\Rightarrow2m^2+\left(a+b\right)m+18=0\)
Để phương trình có nghiệm thì
\(\Delta=\left(a+b\right)^2-144\ge0\)
\(\Leftrightarrow\left|a+b\right|\ge12\)
Ta lại có:
\(\left|a\right|+\left|b\right|\ge\left|a+b\right|\ge12\)
Tới đây thì đơn giản rồi nên b tự làm nhé.
PT có nghiệm chung khi \(x^2+ax+8=x^2+x+a\)
\(\Leftrightarrow ax+8-x-a=o\)
\(\Leftrightarrow a\left(x-1\right)-\left(x-1\right)+7=0\)
\(\Leftrightarrow\left(x-1\right)\left(a-1\right)=-7\)
-7=(-1).7=(-7).1
TH1\(\hept{\begin{cases}x-1=-1\\a-1=7\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\a=8\end{cases}}\)thế vào \(x^2+x+a=0\)(thế vào pt trên cx đc nha) có: 8=0(vô lý) loại
TH2 \(\hept{\begin{cases}x-1=-7\\a-1=1\end{cases}}\)(giải như trên) (loại)
TH3\(\hept{\begin{cases}x-1=7\\a-1=-1\end{cases}}\)(loại)
Th4\(\hept{\begin{cases}x-1=1\\a-1=-7\end{cases}}\)=>\(\hept{\begin{cases}x=2\\a=-6\end{cases}}\)thế vào \(x^2+x+a=0\) có \(2^2+2-6=0\) thỏa mãn
Vậy với a=-6 thì 2 pt có nghiệm chng