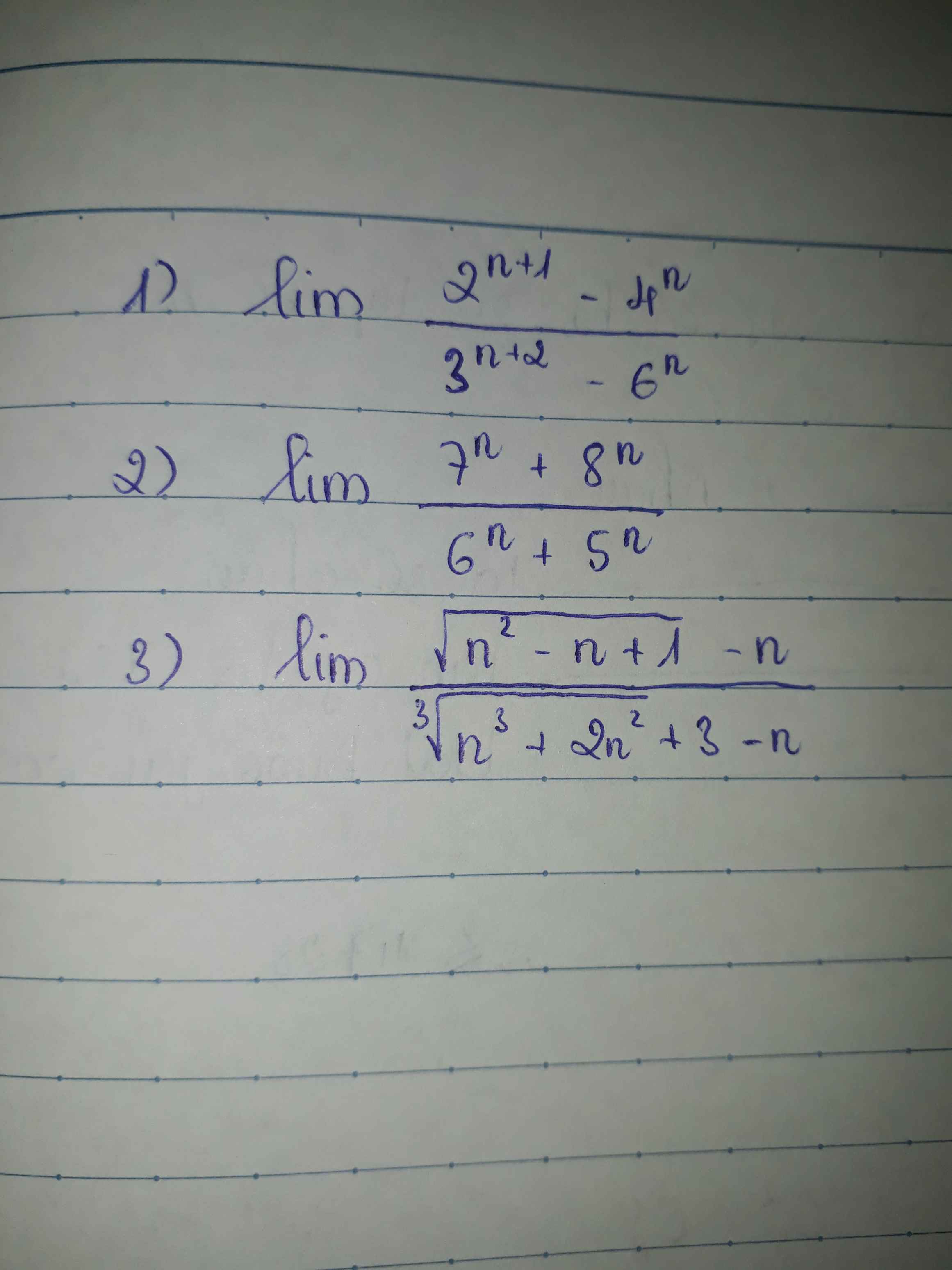mng ơi giúp em help
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2:
a: Xét tứ giác DIHK có
\(\widehat{DIH}=\widehat{DKH}=\widehat{IDK}=90^0\)
Do đó: DIHK là hình chữ nhật
Suy ra: DH=KI(1)
Xét ΔDEF vuông tại D có DH là đường cao ứng với cạnh huyền EF
nên \(DH^2=HE\cdot HF\left(2\right)\)
Từ (1) và (2) suy ra \(IK^2=HE\cdot HF\)

Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.


1. B (-> heavily)
2. D (-> enough food)
3. C (-> because)
4. C (-> hard)
5. B (-> went off)
6. B (-> to walk)
7. A (-> with)
8. C (-> frightening)
9. B (-> due to)
10. A (Jack seldom)
11. A (never goes)
12. C (-> go)
13. A (no sooner had I)
14. C (-> was glass used)
15. B (have I)

a, Theo định luật II Niu tơn
\(\overrightarrow{F_k}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m\cdot\overrightarrow{a}\)
Chiếu lên Oy: \(N=P=mg=20\cdot10=200\left(N\right)\)
Chiếu lên Ox:
\(F_k-F_{ms}=m\cdot a\Rightarrow F_k-\mu N=m\cdot a\Rightarrow60-0,1\cdot200=20\cdot a\Rightarrow a=2\left(\dfrac{m}{s}\right)\)
b, Vận tốc của cái thùng tại điểm D
\(v_D=\sqrt{2as+v_0^2}=\sqrt{2\cdot2\cdot16+4^2}=4\sqrt{5}\left(\dfrac{m}{s}\right)\)
Khi không có tác dụng của lực kéo
Chiếu lên Ox :\(-F_{ms}=m\cdot a'\Rightarrow-N\cdot\mu=m\cdot a'\Rightarrow-200\cdot0,1=20\cdot a'\Rightarrow a'=-1\left(\dfrac{m}{s^2}\right)\)
Thời gian đi được của thùng từ D đến lúc dừng lại
\(t=\dfrac{v-v_D}{a'}=\dfrac{0-4\sqrt{5}}{-1}=4\sqrt{5}\left(s\right)\)

Bài 5:
Gọi độ dài quãng đường là x
Thời gian ô tô thứ nhất đi là x/40(h)
Thời gian ô tô thứ hai đi là x/50(h)
Theo đề, ta có: x/40-x/50=1,5
hay x=300


\(\lim\dfrac{2^{n+1}-4^n}{3^{n+2}-6^n}=\lim\dfrac{2.2^n-4^n}{9.3^n-6^n}=\lim\dfrac{2\left(\dfrac{2}{6}\right)^n-\left(\dfrac{4}{6}\right)^n}{9\left(\dfrac{3}{6}\right)^n-1}=\dfrac{2.0-0}{9.0-1}=0\)
\(\lim\dfrac{7^n+8^n}{6^n+5^n}=\lim\dfrac{\left(\dfrac{7}{8}\right)^n+1}{\left(\dfrac{6}{8}\right)^n+\left(\dfrac{5}{8}\right)^n}=\dfrac{0+1}{0+0}=\dfrac{1}{0}=+\infty\)
Câu 3 là con số 3 dưới mẫu ở trong hay ngoài căn vậy nhỉ?


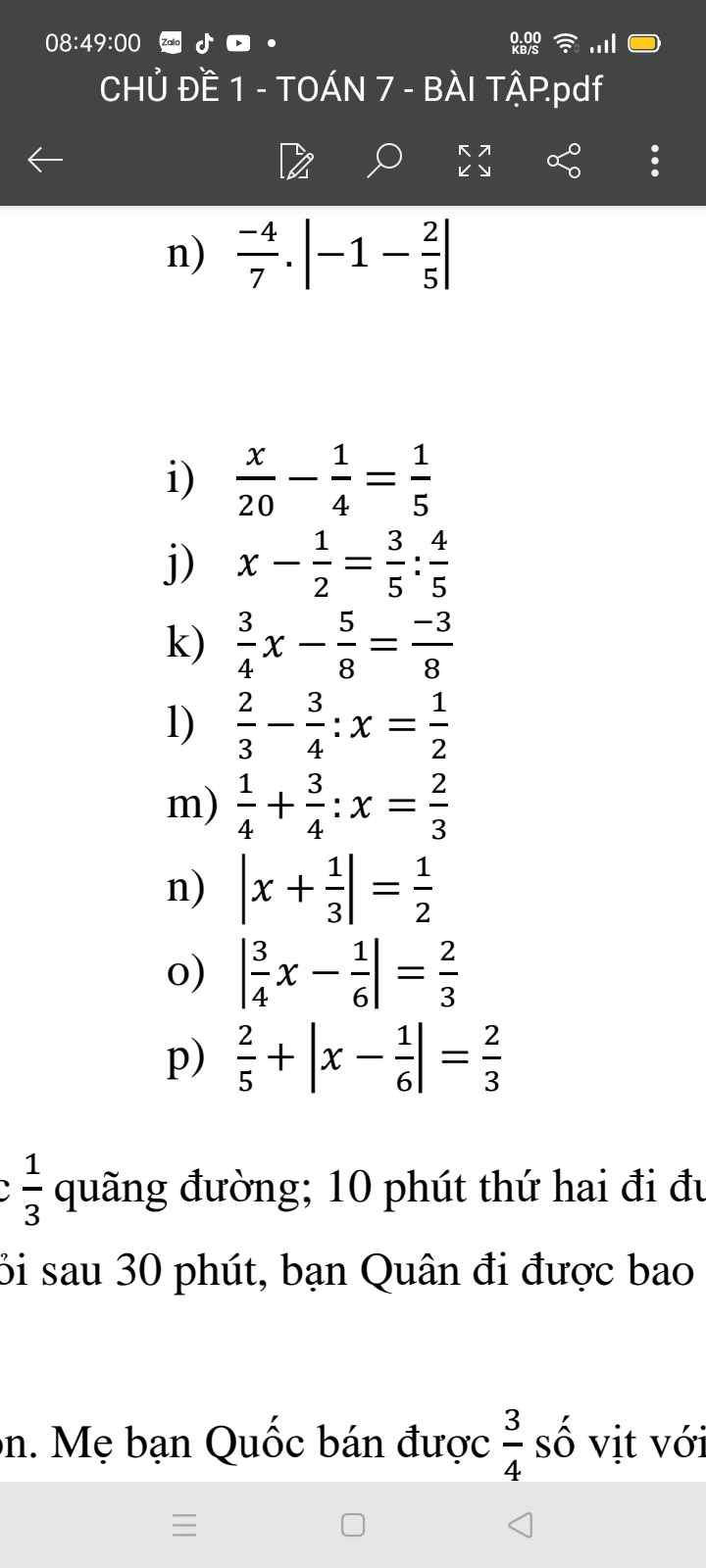


 giúp em vs mng ơi
giúp em vs mng ơi