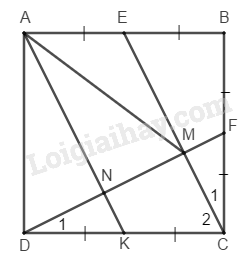
Cho hình vuông ABCD. Qua đểm M thuộc AC kẻ ME⊥MA,MF⊥CD.Chứng minh rằng:
a) BE⊥AF
b)BM⊥EF
c) Các đường thẳng BM,AF,CE đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 11 2022
a: Gọi giao của BM với EF là I, FM và AB là K
Vì ΔADF=ΔBAE(cạnh huyền-cạnh góc vuông)
nên góc DAF=góc ABE
=>góc ABE+góc BAF=góc DAF+góc BAF
=>góc ABE+góc BAF=90 độ
=>AF vuông góc với EB
b: Vì ABCD là hình vuông
nên AC là phân giác của góc BAD
Xét tứ giác AKME có
AK//ME
MK//AE
AM là phân giác của góc KAE
góc KAE=90 độ
Do đó: AKME là hình vuông
=>MK=ME và KB=MF
=>ΔKMB=ΔMEF
=>góc MFE=góc KBM
mà góc KMB=góc IMF
nên góc MFE+góc IMF=góc KBM+góc KMB=90 độ
=>BM vuông góc với EF
c: Xét ΔBEF có
BM,AF là các đường cao
nên BM cắt AF tại trực tâm của tam giác
=>M là trực tâm
=>BM,AF,CE đồng quy
17 tháng 11 2022
a: Gọi giao của BM với EF là I, FM và AB là K
Vì ΔADF=ΔBAE(cạnh huyền-cạnh góc vuông)
nên góc DAF=góc ABE
=>góc ABE+góc BAF=góc DAF+góc BAF
=>góc ABE+góc BAF=90 độ
=>AF vuông góc với EB
b: Vì ABCD là hình vuông
nên AC là phân giác của góc BAD
Xét tứ giác AKME có
AK//ME
MK//AE
AM là phân giác của góc KAE
góc KAE=90 độ
Do đó: AKME là hình vuông
=>MK=ME và KB=MF
=>ΔKMB=ΔMEF
=>góc MFE=góc KBM
mà góc KMB=góc IMF
nên góc MFE+góc IMF=góc KBM+góc KMB=90 độ
=>BM vuông góc với EF
c: Xét ΔBEF có
BM,AF là các đường cao
nên BM cắt AF tại trực tâm của tam giác
=>M là trực tâm
=>BM,AF,CE đồng quy
17 tháng 11 2022
a: Gọi giao của BM với EF là I, FM và AB là K
Vì ΔADF=ΔBAE(cạnh huyền-cạnh góc vuông)
nên góc DAF=góc ABE
=>góc ABE+góc BAF=góc DAF+góc BAF
=>góc ABE+góc BAF=90 độ
=>AF vuông góc với EB
b: Vì ABCD là hình vuông
nên AC là phân giác của góc BAD
Xét tứ giác AKME có
AK//ME
MK//AE
AM là phân giác của góc KAE
góc KAE=90 độ
Do đó: AKME là hình vuông
=>MK=ME và KB=MF
=>ΔKMB=ΔMEF
=>góc MFE=góc KBM
mà góc KMB=góc IMF
nên góc MFE+góc IMF=góc KBM+góc KMB=90 độ
=>BM vuông góc với EF
c: Xét ΔBEF có
BM,AF là các đường cao
nên BM cắt AF tại trực tâm của tam giác
=>M là trực tâm
=>BM,AF,CE đồng quy
VM
15 tháng 11 2019
Nguồn: loigiaihay.com
Bài 1:
Mà \(AD=AB\) (vì \(ABCD\) là hình vuông).
=> \(AM=AB\left(đpcm\right).\)
Chúc bạn học tốt!
a: Gọi giao của BM với EF là I, FM và AB là K
Vì ΔADF=ΔBAE(cạnh huyền-cạnh góc vuông)
nên góc DAF=góc ABE
=>góc ABE+góc BAF=góc DAF+góc BAF
=>góc ABE+góc BAF=90 độ
=>AF vuông góc với EB
b: Vì ABCD là hình vuông
nên AC là phân giác của góc BAD
Xét tứ giác AKME có
AK//ME
MK//AE
AM là phân giác của góc KAE
góc KAE=90 độ
Do đó: AKME là hình vuông
=>MK=ME và KB=MF
=>ΔKMB=ΔMEF
=>góc MFE=góc KBM
mà góc KMB=góc IMF
nên góc MFE+góc IMF=góc KBM+góc KMB=90 độ
=>BM vuông góc với EF
c: Xét ΔBEF có
BM,AF là các đường cao
nên BM cắt AF tại trực tâm của tam giác
=>M là trực tâm
=>BM,AF,CE đồng quy