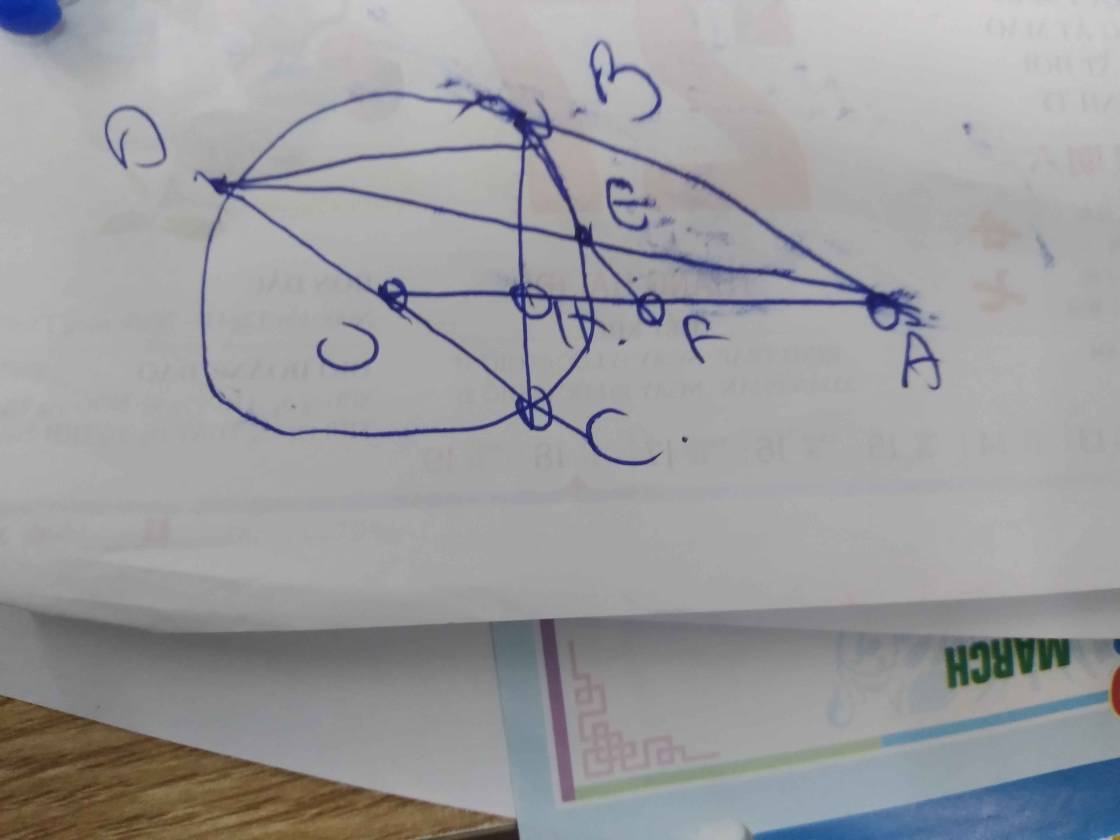
cho hình chữ nhật ABCD. Đường thẳng d ⊥ AC tại C. Đường thẳng AB cắt d tại E và đường thẳng AD cắt đường thẳng d tại f a) CM \(\dfrac{AE^2}{AF^2}=\dfrac{CE}{CF}\) b) BD3 =BE.DF.EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PA
8 tháng 12 2016
AE = CF (gt)
mà AE // CF (ABCD là hình chữ nhật)
=> AECF là hình bình hành
=> FA // CE
=> AFD = ECF (2 góc đồng vị)
mà ECF = CEB (2 góc so le trong, AB // CD)
=> AFD = CEB (1)
AB = CD (ABCD là hình chữ nhật)
mà AE = CF (gt)
=> AB - AE = CD - CF
=> EB = DF (2)
Xét tam giác NEB và tam giác MFD có:
NEB = MFD (theo 1)
EB = FD (theo 2)
EBN = FDM (2 góc so le trong, AB // CD)
=> Tam giác NEB = Tam giác MFD (g.c.g)
=> BN = DM (2 cạnh tương ứng)
O là trung điểm của BD (3)
=> O là trung điểm của AC (ACBD là hình chữ nhật) (4)
=> O là trung điểm của EF (AECF là hình bình hành) (5)
AEI = ABD (2 góc so le trong, EI // BD)
CFK = CDB (2 góc so le trong, FK // BD)
mà ABD = CBD (2 góc so le trong, AB // CD)
=> AEI = CFK (6)
EI // BD (gt)
FK // DB (gt)
=> EI // FK (7)
Xét tam giác EAI và tam giác FCK có:
IEA = KFC (theo 6)
EA = FC (gt)
EAI = FCK (= 900)
=> Tam giác EAI = Tam giác FCK (g.c.g)
=> EI = FK (2 cạnh tương ứng)
mà EI // FK (theo 7)
=> EIFK là hình bình hành
mà O là trung điểm của EF (theo 5)
=> O là trung điểm của IK (8)
Từ (3), (4), (5) và (8)
=> AC, EF, IK đồng quy tại O là trung điểm của BD
O là trung điểm của AC và BD
=> OA = OC = \(\frac{AC}{2}\)
OB = OD = \(\frac{BD}{2}\)
mà AC = BD (ABCD là hình chữ nhật)
=> OA = OD = OB = OC
=> Tam giác OAD cân tại O
mà AOD = 600
=> Tam giác OAD đều
=> AD = OA = OD
mà AD = 1 cm
AD = BC (ABCD là hình chữ nhật)
=> OA = OD = OC = OB = BC = 1 cm
=> AC = 2OA = 2 . 1 = 2 cm
Xét tam giác BAC vuông tại B có:
\(AC^2=BA^2+BC^2\) (định lý Pytago)
\(AB^2=AC^2-BC^2\)
\(=2^2-1^2\)
\(=4-1\)
= 3
\(AB=\sqrt{3}\)
\(S_{ABCD}=AB\times BC=\sqrt{3}\times1=\sqrt{3}\left(cm^2\right)\)
AH
Akai Haruma
Giáo viên
19 tháng 7 2021
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ADC$:
$\frac{1}{DE^2}=\frac{1}{AD^2}+\frac{1}{DC^2}=\frac{1}{6^2}+\frac{1}{8^2}$
$\Rightarrow DE=4,8$ (cm)
Áp dụng hệ thức lượng trong tgv với tam giác $ADF$:
$AD^2=DE.DF$
$6^2=4,8.DF\Rightarrow DF=7,5$ (cm)
$EF=DF-DE=7,5-4,8=2,7$ (cm)
Tiếp tục áp dụng hệ thức lượng trong tgv $ADF$:
$AE^2=DE.DF=4,8.2,7=12,96\Rightarrow AE=3,6$ (cm)
$AF=\sqrt{AE^2+EF^2}=\sqrt{3,6^2+2,7^2}=4,5$ (cm) theo định lý Pitago
$BF=AB-AF=CD-AF=8-4,5=3,5$ (cm)
Áp dụng htl trong tgv với tam giác $ADC$:
$DE^2=AE.CE$
$4,8^2=3,6.CE\Rightarrow CE=6,4$ (cm)
