Cho tam giác ABC vuông tại A, phân giác BD. E nằm trên cạnh BC sao cho BE =BA. Gọi F là điểm thuộc tia đối của tia AB sao cho AF =EC. Chứng minh rằng : câu a : DA=DE, câu b BD là đường trung trực của AE. Đây là bài toán của lớp tớ mong các bạn giải cho. Tớ có 20 bạn cần gấp câu này tớ sẽ trao tick cho ai nhanh nhất và vẽ hình LÀM ƠN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2023
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=90 độ
=>DE vuông góc CB
c: BA=BE
DA=DE
=>BD là trung trực của AE
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>F,D,E thẳng hàng
16 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
=>góc ABD=góc EBD
=>BD là phân giác của góc ABE
b: BA=BE
DA=DE
=>BD là trung trực của AE
1 tháng 1 2023
a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đo: ΔBAD=ΔBED
=>DA=DE
b,c: Xét ΔBFC có BA/AF=BE/EC
nên AE//FC
BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
=>BD vuông góc với FC
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
Do đó: ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>D,E,F thẳng hàng
18 tháng 8 2021
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE\(\left(1\right)\)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra BD là đường trung trực của AE
19 tháng 8 2021
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
AF=EC
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D
28 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>DA=DE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>E,D,F thẳng hàng
16 tháng 5 2023
Mình xin phép sửa lại đề (ý c,)
c) Trên tia đối của tia AB lấy điểm F sao cho AF = EC. Chứng minh `Δ`BFC cân
`a,`
Xét `2\Delta` vuông `ABD` và `EBD`:
`\text {BD chung}`
$\widehat {ABD} = \widehat {EBD} (\text {tia phân giác} \widehat {ABE})$
`=> \Delta ABD = \Delta EBD (ch-gn)`
`b,`
Vì `\Delta ABD = \Delta EBD (a)`
`-> \text {DA = DE (2 cạnh tương ứng) (1)}`
Xét `\Delta DEC`:
$\widehat {DEC} = 90^0$
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`-> \text {DC là cạnh lớn nhất}`
`-> \text {DC > DE (2)}`
Từ `(1)` và `(2)`
`-> \text {DC > DA}`
`c,`
Xét `2\Delta` vuông `ABC` và `AFC`:
`\text {AB = AF (gt)}`
$\widehat {BAC} = \widehat {FAC} (=90^0)$
`\text {AC chung}`
`=> \Delta ABC = \Delta AFC (c-g-c)`
`-> \text {BC = FC (2 cạnh tương ứng)}`
Xét `\Delta BFC`:
`\text {BC = FC}`
`-> \Delta BFC` cân tại C.
`d,`
Ta có: FE là đường cao của `\Delta BFC`
`@` Theo tính chất của `\Delta` cân với các đường trong `\Delta`
`-> \text {FE đồng thời cũng là đường trung trực}`
`-> \text {Ba điểm F, D, E thẳng hàng.}`
16 tháng 5 2023
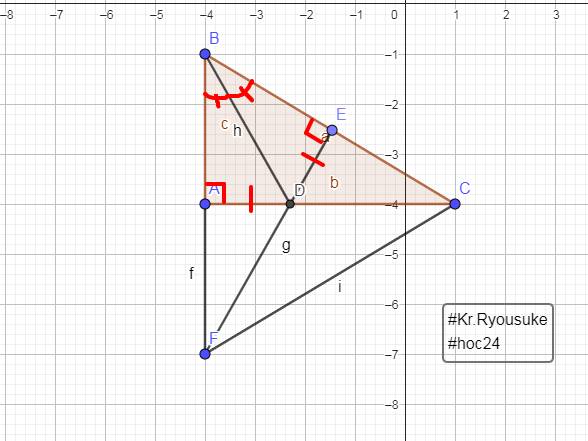
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: DA=DE
DE<DC
=>DA<DC
c: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
AF=EC
=>ΔDAF=ΔDEC
=>DF=DC
=>ΔDFC cân tại D
xin lỗi nhé bạn , mình ko vẽ được trên máy nhưng mình nghĩ vẽ hình ko khó lắm đâu cố nhé
bài giải cách 1
a goi BD giao AE tại I vì AB=EB gt nên B thuộc trung trực AE (tính chất đường trung trực ) nên AI=AE và góc AID= EID =90 độ
chứng minh được tam giác AID=EID ( C-G-C) NÊN AD=ED
câu b AB=AE gt AD=AE câu a nên BD LÀ ĐƯỜNG TRUNG TRỰC AE (tính chất đường trung trực )
cách 2
a) chứng minh tam giác ABD= EBD c g c nên góc A= BED =90 độ và AD=AE từ đó chứng minh được tam giác ADF=EDC g-c-g suy ra AD=AE
Phần b chứng minh như cách 1