Cho 1 tam giác vuông có cách cạnh góc vuông lần lượt là 7cm và 24 cm kẻ đường cao tương ứng với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 8 2021
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=7^2+24^2=625\)
hay BC=25(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có HA là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=6.72\left(cm\right)\\BH=1.96\left(cm\right)\\CH=23.04\left(cm\right)\end{matrix}\right.\)
9 tháng 9 2016
Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)
CM
9 tháng 7 2017
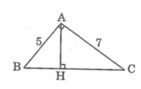
Giả sử tam giác ABC có 
, AB = 5, AC = 7
Theo định lí Pi-ta-go, ta có:
B C 2 = A B 2 + A C 2
⇒ BC = 
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
AH.BC = AB.AC ⇒ AH = 
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
A
B
2
=
B
H
.
B
C
⇒ BH =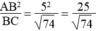 
CH = BC – BH =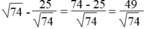 
TD
19 tháng 7 2017
áp dụng hệ thức: \(\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}\)=> \(\frac{1}{h^2}=\frac{1}{25}+\frac{1}{49}=\frac{74}{1225}\)=>\(h=\frac{35\sqrt{74}}{74}\left(cm\right)\)
áp dụng hệ thức: ab=hc (c là cạnh huyền) => \(35=c\frac{35\sqrt{74}}{74}\)=>\(c=\sqrt{74}\)(cm)
áp dụng hệ thức hình chiếu: =>a'=\(\frac{25\sqrt{74}}{74}\left(cm\right)\)=>b'=\(\frac{49\sqrt{74}}{74}\left(cm\right)\)
CM
1 tháng 5 2017
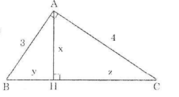
ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.
Theo định lí Pitago ta có:
Mặt khác, A B 2 = B H . B C (định lí 1)
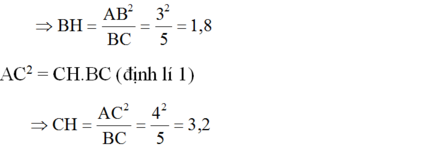
Theo định lí 3 ta có: AH.BC = AB.AC
CM
21 tháng 8 2019
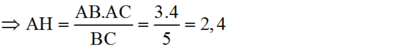
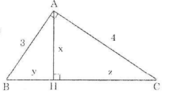
ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.
Theo định lí Pitago ta có:
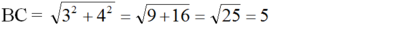
Mặt khác, AB2 = BH.BC (định lí 1)
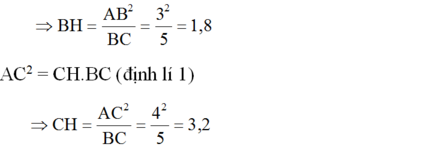
Theo định lí 3 ta có: AH.BC = AB.AC
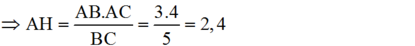
Cho tam giác ABC vuông tại A, AH là đường cao. AB = 24cm, AC = 7cm.
Áp dụng định lý Pytago ta có: \(BC=\sqrt{AC^2+AB^2}=\sqrt{7^2+24^2}=25.\)
Áp dụng hệ thức lượng ta có:
\(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{24.7}{25}=6.72\)
\(AC^2=HC.BC\Rightarrow HC=\frac{AC^2}{BC}=\frac{7^2}{25}=1,96\)
\(\Rightarrow HB=BC-HC=25-1.96=23.04\)